POJMOVNIK - S
Sastav atmosfere
- Atmosferu s obzirom na sastav dijelimo na homosferu i heterosferu. Donjih 80 km atmosfere nazivamo homosferom. U homosferi su volumni odnosi pojedinih kvazipermanentnih plinova konstantni, dok se količina ostalih sastojaka mijenja. U heterosferi, koja se nalazi iznad homosfere, volumni odnosi atmosferskih plinova variraju, zbog fotodisocijacije uzrokovane ultraljubičastim (UV) i rendgenskim Sunčevim zračenjem. U heterosferi se djelovanjem UV zračenja događa fotodisocijacija molekularnog kisika (O2). Stoga koncentracija O2 opada visinom, a koncentracija atomskog kisika (O) raste. Već na 130 km visine, samo jedna trećina kisika nalazi se u molekularnoj formi, dok se na 500 km visine gotovo sav kisik nalazi u atomskoj formi. Molekularni dušik (N2) se teže disocira. Stoga je na 500 km visine koncentracija atomskog dušika (N) mala.U visokoj atmosferi sastojci zraka apsorbiraju UV zračenje te se zbog toga ioniziraju. Iznad 60 km visine u atmosferi se nalazi puno više iona nego u manjim visinama. Gustoća elektrona maksimalna je na visinama između 250-500 km, stoga se taj dio atmosfere naziva ionosfera. Ionosfera utječe na propagaciju radiovalova, ali za meteorološke procese nije važna.
Tablica 1. Sastav čistog zraka u donjoj atmosferi.
| plin | molekularna masa | volumni udio (%) | maseni udio (%) | boravak u atmosferi | |
| gotovo konstantan omjer | O2, kisik | 32.00 | 20.95 | 23.1 | 5•103 god. |
| N2, dušik | 28.01 | 78.09 | 75.5 | 106 god. | |
| Ar, argon | 39.95 | 0.93 | 1.3 | ||
| Ne, neon | 20.18 | 1.8•10-3 | 1.3•10-3 | ||
| He, helij | 4.01 | 5.2•10-4 | 7.2•10-5 | 107 god. | |
| Kr, kripton | 83.80 | 1.1•10-4 | 3.3•10-4 | ||
| Xe, ksenon | 131.30 | 8.6•10-6 | 3.9•10-5 | ||
| Rn, radon | 222.00 | 6.0•10-18 | |||
| promjenjiv omjer | CO2, ugljikov dioksid | 44.01 | 3.6•10-2 | 4.6•10-2 | 5-6 god. |
| CH4,metan | 16.04 | 1.4•10-4 | 7.8•10-5 | 4-7 god. | |
| H2, vodik | 2.01 | 5•10-5 | 3.5•10-6 | 6-8 god. | |
| N2O, dušikov oksid | 44.01 | 1•10-7 | 3.1•10-7 | 25 god. | |
| O3, ozon | 48.00 | 2•10-6 | 6•10-6 | 10 god. | |
| jako promjenjiv omjer | H2O, vodena para | 18.02 | ≤ 4.0 | 10 dana | |
| CO, ugljikov monoksid | 28.01 | 1•10-5 | 2•10-5 | 0.2-0.5 god. | |
| NO2, dušikov dioksid | 46.01 | 2.3 - 3.5•10-5 | 8-10 dana | ||
| NH3, amonijak | 17.03 | 1•10-6 | 1•10-6 | 5 dana | |
| SO2, sumporov dioksid | 64.06 | 2•10-8 | 9•10-8 | 2 dana | |
| H2S, sumporovodik | 34.08 | ≤ 0.6•10-7 | 0.5 dana | ||
| organski ugljik (bez CH4 i halogenougljika) | 2 dana |
Ozon (O3) se u znatnijim količinama nalazi u višoj atmosferi i to u visinama od oko 10 do 50 km. Taj sloj više atmosfere zove se ozonosfera. Ozon u višoj atmosferi nastaje u dva koraka. U prvom koraku, molekula kisika apsorbira UV Sunčevo zračenje, te stoga fotodisocira:
O2 + hν ![]() O + O,
O + O,
gdje je hν energija fotona UV zračenja, čije su valne duljine manje od 240 nm (1 nm = 10-9 m), h je Planckova konstanta h = 6.625•10-34 J s, a ν je frekvencija zračenja (s-1). U drugom koraku uz prisustvo trećeg tijela (M) dolazi do sudara (kolizije) atoma i molekule kisika:
O2 + O + M ![]() O3 + M.
O3 + M.
Do kolizije najčešće dolazi na visinama do oko 50 km, budući da u tom području još uvijek ima dovoljno kisika u molekularnoj formi. Istovremeno, ozon se i sam raspada zbog fotodisocijacije:
O3 + hν ![]() O2 + O.
O2 + O.
Međutim, za fotodisocijaciju ozona odgovorne su valne duljine u rasponu od 200 do 300 nm.
Najviše ozona nastaje u tropima na visinama iznad 25 km. To je područje u kojem je postignuta ravnoteža između raspoloživog kisika (čija koncentracija opada visinom) i Sunčevog UV zračenja (koje raste visinom). Ozon se atmosferskim gibanjima prenosi prema polovima. Stoga se najviše ozona (~ 6 . 1012 molekula po cm3) nalazi u tropima na visini od 25 km, dok je nad polovima maksimum na 18 km visine.
Premda je količina ozona u atmosferi relativno mala (maksimalne koncentracije ne prelaze 10 ppm, njegova važnost za život na Zemlji je ogromna. Osim ozona ni jedan od preostalih sastojaka atmosfere ne apsorbira UV zračenje u rasponu od 240 do 290 nm (vidi radijacijsko-apsorpcijska svojstva sustava Zemlja-atmosfera. Ozon međutim apsorbira gotovo svu radijaciju u tom dijelu spektra. Kad bi to zračenje došlo do Zemljine površine, oštetilo bi genetički materijal, a fotosinteza, koja je neophodna za biljni svijet, bila bi onemogućena. Nadalje, zbog svojih apsorpcijskih svojstava ozon ima važnu ulogu u radijacijskoj ravnoteži sustava Zemlja-atmosfera, te utječe na termalnu strukturu atmosfere.
Posljednjih desetljeća puno pažnje pridaje se problemu ozonske rupe. Sredinom sedamdesetih godina 20. stoljeća nad Antarktikom je u ozonosferi uočeno veliko smanjenje koncentracije ozona s obzirom na ranija razdoblja. Kemičari atmosfere pripisuju to smanjenje ljudskom djelovanju, odnosno antropogenoj emisiji klorofluorougljika (CFC, koji su poznati i pod nazivom freoni). Najveće smanjenje (ponegdje čak do 99%) uočeno je na visinama od 14-19 km nad tlom. Kako bi spriječila pogubno djelovanje ozonske rupe na život na Zemlji, međunarodna zajednica ulaže velike napore da se emisija CFC svede na minimum.
Za razliku od ozona u ozonosferi, koji je neophodan za život na Zemlji, ozon pri tlu je je nepoželjan. U manjim količinama iritira očnu sluznicu, grlo, nos i dišne puteve, dok u velikim koncentracijama može biti smrtonosan. Posljednjih desetljeća ozon pri tlu nastaje fotokemijskim reakcijama u urbanoj atmosferi bogatoj dušikovim oksidima NO i NO2 (koji se najčešće kraće označavaju s NOx). NOx, koji su posebno aktivni u atmosferskom ciklusu ozona, u atmosferu dospijevaju u većim količinama kao posljedica ljudskih aktivnosti (naročito prometa). Stoga se u velikim gradovima s gustim prometom, koji obiluju Sunčevim zračenjem, a nalaze se u toplim i suhim klimama (poput npr. Rima, Tokija, Atene i Los Angelesa), javlja onečišćenje zraka poznato pod nazivom fotokemijski smog. U tako onečišćenoj atmosferi uz O3 i NOx nalaze se i organski nitrati, poput PAN-a (peroksiacetil nitrat CH3C(O)OONO2), oksidirani ugljikovodici i tzv. fotokemijski aerosol, a nad gradom se zbog velike količine aerosola može vidjeti žućkasto-smeđi oblak, koji je zbog svog čestog pojavljivanja nad Atenom dobio ime nefos (od grčke riječi νεφοσ, što znači oblak).
Ugljikov dioksid je plin bez mirisa. Teži je od suhog zraka. U našoj atmosferi ga približno ima oko 0.036 %, ili volumno oko 360 ppm (podaci za 1994. godinu), dok je u atmosferama Marsa i Venere glavni sastojak. CO2 dospijeva u atmosferu biološkim i prirodnim procesima (npr. disanjem, fotosintezom, vulkanskim erupcijama i drugim), te sagorijevanjem fosilnih goriva (ugljena i nafte). Zbog apsorpcije Sunčevog zračenja valnih duljina λ < 0.1690 μm atmosferski CO2 disocira u CO i atomski kisik:
CO2 + hν ![]() CO + O.
CO + O.
CO2 je uz vodenu paru jedan od najvažnijih atmosferski apsorbera Zemljinog dugovalnog zračenja. Zbog apsorpcije IC zračenja na molekulama CO2 atmosfera se zagrijava, atmosferski CO2 i sam počinje dugovalno zračiti, te tako doprinosi zagrijavanju Zemljine površine. Stoga CO2 poput ozona i vodene pare također utječe na toplinsku ravnotežu sustava Zemlja-atmosfera. Prema nekim proračunima, kada u atmosferi ne bi bilo CO2, prosječna temperatura Zemljine površine bi sa 15oC pala na -10oC. Koncentracija CO2 najveća je u gradovima, a kako je CO2 teži od zraka, to mu je koncentracija najveća pri tlu.
Danas u atmosferi ima gotovo 30% više CO2 nego prije dvjestotinjak godina, a posljednjih desetljeća porast koncentracije CO2 iznosi čak 0.5 % godišnje. Istovremeno, srednja temperatura pri tlu, gledajući Zemlju u cjelini, u posljednjih stotinjak godina povisila se za oko 0.5oC ± 0.2oC. To globalno zatopljenje najvećim dijelom se pripisuje porastu koncentracije CO2 u atmosferi počev od Industrijske revolucije do danas, ali pospješeno je i antropogenom emisijom drugih apsorbera IC zračenja.
Zahvaljujući rasponu atmosferskih temperatura, vodena tvar se u atmosferi može naći u sva tri agregatna stanja: plinovitom, tekućem i krutom. Vodena para je vrlo varijabilan atmosferski sastojak, a njena količina se mijenja i prostorno i vremenski. Volumno je u atmosferi može biti najviše 4%. Najviše je ima u tropima, a najmanje u polarnom području. Vodena para u atmosferu dospijeva evapotranspiracijom. Kako se evapotranspiracija događa na Zemljinoj površini, koncentracija vodene pare opada s visinom, te se sva vodena para nalazi u prvih dvadesetak km atmosfere. Vodena para vrlo efikasno apsorbira toplinsko zračenje, te i sama zrači dugovalno. Stoga (poput O3 i CO2) bitno utječe na toplinsku ravnotežu sustava Zemlja-atmosfera.
U atmosferi se osim plinova i vodene pare nalaze još i aerosoli. Količina aerosola je i prostorno i vremenski jako varijabilna. Često se u atmosferi nalaze i onečišćujuće tvari.
Vidi radijacijsko-apsorpcijska svojstva sustava Zemlja-atmosfera.
Senzitivna (senzibilna) toplina
- toplina koju uzorak (čest) dobije ili izgubi pri promjeni temperature, a da pri tom agregatno stanje uzorka ostane nepromijenjeno.Vidi latentnu toplinu.
Sila gradijenta tlaka
- sila koja djeluje na česti fluida koje se nalaze u nejednolikom polju tlaka. Pogledajmo infinitezimalni element volumena fluida dV = dxdydz (slika) čije središte se nalazi u točki (x0, y0, z0). Zbog neprestanog slučajnog gibanja molekula fluida na plohe volumena neprestano djeluje impuls od okolnog fluida. Dakle, okolni fluid tlači plohe tlakom koji je jednak impulsu po jedinici površine u jedinici vremena. Ako je tlak u središtu elementa p0, tada tlak koji djeluje na lijevu plohu (pL) možemo prikazati razvojem u Taylorov red oko točke (x0, y0, z0), gdje ćemo zanemarivo male članove višeg reda izostaviti. Dobivamo pL![]()
Kako je sila tlaka koja djeluje na element volumena fluida proporcionalna gradijentu tlaka, a ne magnitudi tlaka, zovemo je sila gradijenta tlaka. Akceleraciju sile gradijenta tlaka ap dobivamo tako da silu podijelimo s masom elementa m = r dV, gdje je r gustoća fluida, a a je specifični volumen (a = 1/r)
![]()
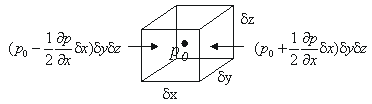
Ilustracija x - komponente sile gradijenta tlaka
Sila teža
- rezultanta gravitacijske i centrifugalne sile. Akceleracija sile teže g je:g = g* + W2 R = - G Mz r-2 (r/r) + W2 R
gdje je g* je vektor akceleracije gravitacije, r je vektor udaljenosti centara masa Zemlje i česti na koju djeluje sila teža, G je gravitacijska konstanta, Mz je masa Zemlje, R je vektor udaljenosti česti od osi rotacije, a W je kutna brzina rotacije Zemlje.
Zbog djelovanja meridionalne komponente sile teže (vidi donju sliku) Zemlja je spljoštena, pa je ekvatorijalni radijus oko 21 km veći od polarnog.
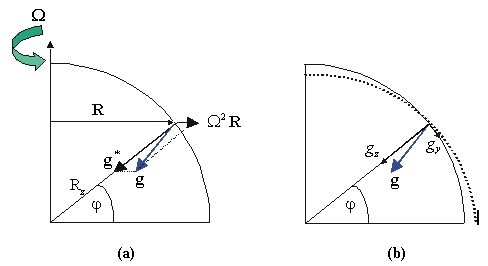
Slika (a) prikazuje akceleraciju sile teže na Zemljinoj površini. Akceleracija sile teže (g) rezultanta je aceleracije sile gravitacije (g*) i centrifugalne akceleracije (W2 R) na geografskoj širini f. Rz je srednji radijus Zemlje. Slika (b) ilustrira razlog spljoštenosti Zemlje. Akceleraciju sile teže možemo rastaviti na komponentu usmjerenu prema središtu Zemlje (gz) i na meridionalnu komponentu, orijentiranu prema ekvatoru (gy). Komponenta gy uzrokuje spljoštenost Zemlje. Zemljina površina prikazana je crtkanom krivuljom.
Vrijednost akceleracije sile teže vrlo malo se mijenja s promjenom položaja česti (tj. s nadmorskom visinom i s geografskom širinom). Stoga u meteorologiji najčešće pretpostavljamo da je njezin iznos konstantan g = g0:
g0 = 9.81 m s-2.
Sila trenja
- Trenje postoji u svakom realnom fluidu. U atmosferi utječe na vrijeme i klimu tako da usporava strujanje i zakreće vektor vjetra. U atmosferi je najvažnije je u najdonjem, atmosferskom graničnom sloju, dakle u prvih približno 1-2 km. Pod trenjem podrazumijevamo bilo koji od više fizikalnih procesa koji mijenjaju brzinu (odnosno impuls fluida. Ti procesi uključuju prijenos impulsa u viskoznom fluidu, tokove preko prepreka, valna gibanja, te naročito kompliciran i širok spektar kaotične turbulencije. Da bi matematički prikazali (parametrizirali) silu trenja, moramo najprije objasniti dva pojma, a to su uspor trenjem i napetost.Trenje se općenito opire relativnom gibanju fluida. Tako npr., ako zrak struji preko čvrste prepreke (npr. planine), trenje će se opirati strujanju. (Ovaj uobičajeni koncept potezanja trenjem katkad se pogrešno primijenjuje i na slojeve fluida koji nisu u direktnom kontaktu sa čvrstom preprekom.) Efekt potezanja prepreke, tzv. tlak potezanja, nastaje zbog razlika u tlaku duž prepreke, budući da je u navjetrini prepreke tlak veći nego u zavjetrini. Uspor kojim prepreka djeluje na strujanje suprotnog je smjera od samog strujanja. Kako prepreka 'poteže' vjetar u smjeru suprotnom od smjera vjetra, to onda zbog trećeg Newtonovog zakona gibanja vjetar mora 'potezati' prepreku u smjeru samog strujanja. Sila kojom vjetar 'poteže' prepreku proporcionalna je CV2, gdje je C koeficijent potezanja, a V je modul brzine vjetra. Princip akcije i reakcije ukazuje na to da dva tijela mogu međusobno razmijenjivati impuls tako da, gledajući oba tijela kao jedinstveni sustav, impuls sustava ostaje sačuvan.
Potezanja prepreke (koje je suprotnog smjera od strujanja) i silu reakcije (koja je istog smjera kao i strujanje) možemo ilustrirati npr. drvetom koje se savilo zbog zapuha vjetra. Drvo se savilo zbog sile trenja zraka (sile reakcije), koja je suprotnog smjera od sile trenja kojom prepreka djeluje na zrak. Slično, oborinski elementi (kristali leda i kapljice kiše) gibaju se relativno prema dolje u odnosu na okoliš zbog sile teže. Na njih djeluje sila potezanja prema gore (reakcija zraka). Stoga mora postojati sila prema dolje kojom oborinski elementi djeluju na zrak. Na taj način snažna oborina u oluji sama umanjuje uzlazne struje, a pojačava silazne struje.
Osim uspora trenjem, kojim se strujanje odupire prepreci, u fluidu postoji i trenje na velikim udaljenostima od prepreka. Stoga uvodimo pojam tangencijalne napetosti. Tangencijalna napetost je sila po jedinici površine, koja je analogna sili između dva vertikalno učvršćena kruta tijela, koja se horizontalno gibaju različitim brzinama. Sile koje dijeluju na oba tijela, odupiru se relativnom gibanju, akcelerirajući sporije i usporavajući brže tijelo. Na taj način napetost djeluje tako da prenosi impuls duž ploha koje su okomite na smjer gibanja. Slično, kod fluida čiji se slojevi gibaju različitim brzinama, dolazi zbog postojanja tangencijalne napetosti do razmjene impulsa.
Napetost je tenzor drugog reda (vidi sliku), a može se pisati u matričnom obliku
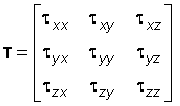 ,
(1)
,
(1)
gdje su txx, tyy i tzz komponente tlaka u x, y i z smjeru, a preostalih 6 komponenti su tangencijalne napetosti.
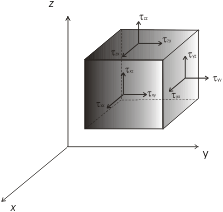
Ilustracija tenzora napetosti koji djeluje na plohe elementa volumena fluida. Zbog preglednosti slike prikazane su samo komponente napetosti koje djeluju na tri osjenčane plohe. Prvi indeks (i) u komponenti napetosti tij pokazuje na koju os je okomita promatrana ploha, a drugi indeks (j) pokazuje u kojem smjeru djeluje napetost na promatranu plohu. Tangencijalne napetosti su one za koje je i <> j, a txx, tyy i tzz su komponente tlaka u x, y i z smjeru.
Tangencijalnu napetost duž granice sloja fluida uzrokuju viskoznost, turbulencija i valovi. Sva tri uzroka tangencijalne napetosti u sebi uključuju procese čije su skale vrlo male u odnosu na dimenzije sloja fluida. Molekularna viskoznost je unutarnje trenje kojim se realni fluid odupire gibanju. U slučaju atmosfere viskoznost je mjera efikasnosti kojom pojedini slojevi zraka razmjenjuju impuls. Do razmjene impulsa dolazi naglim, gotovo slučajnim molekularnim gibanjima, a rezultat toga je smanjivanje razlika u impulsu koje postoji među slojevima - zbog razmjene impulsa brži slojevi se usporavaju, a sporiji ubrzavaju. Molekularna viskoznost važna je samo u prvih nekoliko milimetara uz Zemljinu površinu, te u tankom sloju oko oborinskih elemenata (kapljica i kristala) unutar oblaka. Stoga je u većini meteoroloških istraživanja najčešće zanemarujemo.
Turbulencija je najvažniji izvor napetosti trenja. Kod turbulencije miješanje postoji zbog kaotičnih turbulentnih vrtloga, koji se javljaju u širokom rasponu skala. Vrtlozi nastaju u srednjem toku i bivaju njime prenošeni s jednog mjesta na drugo. Turbulencija postoji i u atmosferi i u oceanu. Zbog turbulentnih vrtloga individualne česti fluida slučajno se gibaju i prema gore i prema dolje, pa različiti slojevi međusobno razmjenjuju česti. Ako u toku postoji vertikalno smicanje (promjena brzine visinom), tada česti koje potječu iz različitih slojeva imaju različite impulse. Stoga se zbog slučajne razmjene česti razmjenjuje i impuls. Ovaj proces je analogan razmjeni impulsa pri viskoznoj napetosti, ali je kod turbulentne napetosti tipični pomak česti, koji nazivamo duljina miješanja puno veći od pomaka molekula zbog viskoznosti.
Turbulentna napetost u sloju trenja (u atmosferi to je atmosferski granični sloj vrlo često se aproksimira izrazom
t = rK
![]() u/
u/![]() z,
(2)
z,
(2)
gdje je t napetost, ![]() u/
u/![]() z
je smicanje, u je brzina, z je visina, a r
gustoća fluida. Koeficijent K naziva se vrtložna ili turbulentna viskoznost i općenito ovisi o strujanju, te ima veće vrijednosti pri većem smicanju brzine. Takav pristup tretiranju
turbulencije naziva se K-teorija.
K-teorija je zadovoljavajuća aproksimacija ako turbulencija nastaje zbog smicanja. Međutim, ako se turbulencija javi kao posljedica konvekcije (uzgona), jednadžbe poput ove ne mogu se primijeniti.
z
je smicanje, u je brzina, z je visina, a r
gustoća fluida. Koeficijent K naziva se vrtložna ili turbulentna viskoznost i općenito ovisi o strujanju, te ima veće vrijednosti pri većem smicanju brzine. Takav pristup tretiranju
turbulencije naziva se K-teorija.
K-teorija je zadovoljavajuća aproksimacija ako turbulencija nastaje zbog smicanja. Međutim, ako se turbulencija javi kao posljedica konvekcije (uzgona), jednadžbe poput ove ne mogu se primijeniti.
Impuls se može vertikalno razmijenjivati i pomoću internih težinskih valova. Napetost valova može se u atmosferi propagirati i do tropopauze.
Da bi na element volumena fluida djelovala neto sila trenja u horizontalnom smjeru, mora postojati razlika u napetosti duž vertikale. Stoga se kod proučavanja graničnog sloja atmosfere i oceana horizontalna komponenta akceleracije zbog sile trenja često prikazuje u obliku
atr = r-1
![]() t
/
t
/![]() z,
(3)
z,
(3)
gdje je t napetost, r je gustoća fluida, a z vertikalna koordinata.
Gornji izraz za akceleraciju zbog sile trenja možemo poopćiti na trodimenzionalni slučaj u kojem tenzor napetosti T ima 9 komponenti (vidi jednadžbu (1)). Akceleracija sile trenja tada je vektor s komponentama (atr)x, (atr)y i (atr)z u x, y i z smjeru
(atr)x = r-1
( ![]() t
xx/
t
xx/![]() x +
x +
![]() t
yx/
t
yx/![]() y +
y +
![]() t
zx/
t
zx/![]() z)
z)
(atr)y = r-1
( ![]() t
xy/
t
xy/![]() x +
x +
![]() t
yy/
t
yy/![]() y +
y +
![]() t
zy/
t
zy/![]() z)
(4).
z)
(4).
(atr)z = r-1
( ![]() t
xz/
t
xz/![]() x +
x +
![]() t
yz/
t
yz/![]() y +
y +
![]() t
zz/
t
zz/![]() z)
z)
U slučaju molekularne viskoznosti uobičajeno je pretpostaviti da se fluid ponaša poput
Newtonovog fluida je tij
= m ![]() uj/
uj/![]() xi, gdje je
m koeficijent dinamičke viskoznosti (kg m-1s-1). Koeficijent dinamičke viskoznosti neznatno se mijenja temperaturom, pa se najčešće koristi konstantna vrijednost
m = 1.8 . 10-5 kg m-1s-1 (za atmosferu) i
m = 1.8 . 10-3 kg m-1s-1 (za vodu).
xi, gdje je
m koeficijent dinamičke viskoznosti (kg m-1s-1). Koeficijent dinamičke viskoznosti neznatno se mijenja temperaturom, pa se najčešće koristi konstantna vrijednost
m = 1.8 . 10-5 kg m-1s-1 (za atmosferu) i
m = 1.8 . 10-3 kg m-1s-1 (za vodu).
Uvrstimo li komponente tenzora napetosti za Newtonov fluid u jednadžbu (4), za x – komponentu akceleracije dobivamo
(atr)x = r-1 (
![]() t
xx/
t
xx/![]() x+
x+![]() t
yx/
t
yx/![]() y+
y+![]() t
zx/
t
zx/![]() z )
= r-1 (m
z )
= r-1 (m ![]() 2u/
2u/![]() x2+m
x2+m
![]() 2u/
2u/![]() y2+m
y2+m
![]() 2u/
2u/![]() z2) =
m r-1
z2) =
m r-1 ![]() 2u.
2u.
Analogno dobivamo za y i z smjer: (atr)y =
m r-1 ![]() 2v
i (atr)z = m r-1
2v
i (atr)z = m r-1
![]() 2w. Dakle, za
Newtonov fluid akceleracija zbog molekularnog trenja može se pisati vektorski
2w. Dakle, za
Newtonov fluid akceleracija zbog molekularnog trenja može se pisati vektorski
atr = m r-1
![]() 2v
= n
2v
= n ![]() 2v,
(5)
2v,
(5)
gdje je v vektor brzine fluida s komponentama u, v i w, a koeficijent n = m r-1 je koeficijent kinematičke viskoznosti (m2 s-1).
Zemljina površina približno je horizontalna. Stoga su najizraženiji efekti trenja oni, koji postoje zbog prijenosa molekularnog impulsa duž vertikale, budući da je on puno je veći od prijenosa impulsa duž horizontale. Posljedica toga su vertikalne varijacije vjetra, koje su puno veće od horizontalnih varijacija. Uzmemo li u obzir efekte molekularnog trenja, koji postoje samo zbog prijenosa impulsa duž vertikale, jednadžba (5) se pojednostavnjuje
atr = n
![]() 2v/
2v/![]() z2.
(6)
z2.
(6)
Želimo li u Newtonovom drugom zakonu gibanja uvažiti turbulentno trenje, poslužiti ćemo se Prandtlovom relacijom koja je izvedena po analogiji na molekularno trenje, a uvažava prijenos impulsa turbulentnim vrtlozima samo duž vertikale
atr = me
r-1 ![]() 2v/
2v/![]() z2,
(7)
z2,
(7)
gdje je v vremenski srednjak vektora brzine, a me je koeficijent vrtložne (ili turbulentne) viskoznosti. Koeficijent turbulentne viskoznosti me nije jednostavan poput koeficijenta dinamičke viskoznosti m, koji ovisi samo o temperaturi. Za razliku od m, koeficijent turbulentne viskoznosti me ovisi i o vertikalnom temperaturnom gradijentu, te o hrapavosti podloge i varijacijama gustoće.
Vremenski srednjak vektora brzine v je takav da je brzina v u svakom trenutku jednaka srednjoj brzini uvećanoj za turbulentno poremećenje v' , odnosno v = v + v'.
Sinoptička karta
- zemljopisna karta na kojoj su prikazani meteorološki podaci u nekom trenutku nad velikim područjem (npr. nad Europom). Sinoptička karta može biti dijagnostička (prikazuje postojeće stanje atmosfere na temelju analize mjerenih podataka, vidi sliku 1) ili prognostička (prikazuje očekivano stanje atmosfere u nekom budućem trenutku, a temelji se na rezultatima prognostičkog numeričkog modela, vidi sliku 2). Podaci na sinoptičkoj karti prikazani su brojevima, znakovima ili izolinijama.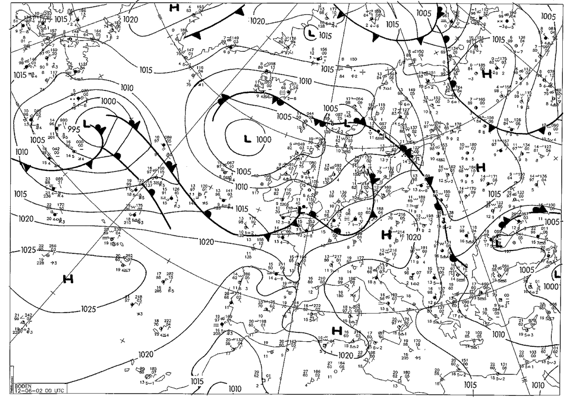
Slika 1. Prizemna sinoptička karta nad Europom. Ova karta rezultat je analize izmjerenih podataka te opisuje postojeće stanje u analiziranom trenutku (12. lipnja 2000. u 12 UTC). Stoga je dijagnostička.
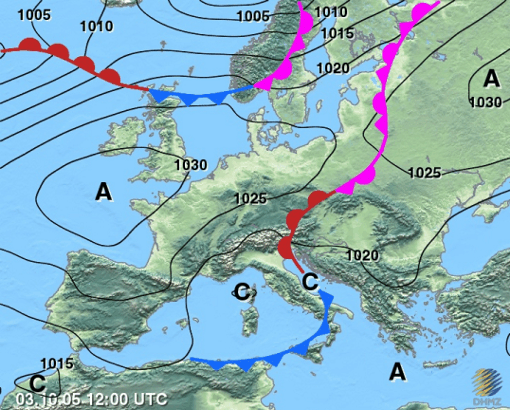
Slika 2. Prognostička prizemna karta Državnog hidrometeorološkog zavoda. Prognoza se odnosi na 3. listopada 2005, a izračunata je prethodnog dana numeričkim modelom. Prikazano je polje tlaka uz pripadne ciklone i anticiklone te fronte.
Vidi sinoptička meteorologija, sinoptička skala.
Sinoptička meteorologija
- dio meteorologije koji se bavi analizom i prognozom vremena.Sinoptička postaja
- postaja na kojoj se mjere i opažaju meteorološki elementi (tlak, temperatura, naoblaka i drugo) za potrebe analize i prognoze vremena. Motranja na sinoptičkoj postaji obavljaju se u glavnim sinoptičkim terminima: 0000, 0600, 1200 i 1800 UTC, a na nekim postajama i u međuterminima: 0300, 0900, 1500, 2100 UTC. Podaci sa svih sinoptičkih postaja šalju se u državni centar odakle dalje idu u međunarodnu razmjenu. Sinoptička postaja ujedino je i klimatološka.Vidi sinoptička meteorologija.
Sinoptička skala
- prostorno-vremenska skala koja je karakteristična za baričke sustave umjerenih širina, poput ciklone, anticiklone, doline, grebena. Opažanjem su u umjerenim širinama uočene ovi tipični redovi veličina varijabli na sinoptičkoj skali:
| U ~ 10 m s-1 | skala horizontalne brzine |
| W ~ 1 cm s-1 | skala vertikalne brzine |
| L ~ 106 m | skala duljine |
| H ~ 104 m | skala visine |
| dP/r ~ 103 m2 s-2 | skala horizontalnih fluktuacija tlaka |
| L/U ~ 105 s | horizontalna skala vremena |
stoga se te vrijednosti koriste pri postupku analize skala pri teorijskom istraživanju i numeričkom modeliranju sinoptičkih procesa.
Slobodna konvekcija
- dizanje zraka koje postoji samo zbog labilnosti te za koje nije potrebna prisila.Čest koja je uvjetno nestabilna (ds < g < dd) može zbog prisilnog dizanja postati nestabilna. Takva čest posjeduje latentnu nestabilnost.
Promatramo uvjetno nestabilnu nezasićenu čest (vidi sliku) koja se u početku nalazi u točki A. Prilikom dizanja (npr. pri prijelazu preko topografske prepreke), čest se hladi suhoadijabatski jer je nezasićena. Čest će se hladiti suhoadijabatski sve dok ne dođe do kondenzacijske razine B, koja je na visini zk. Dalje, ako se nastavi dizati, čest će se hladiti mokroadijabatski. Kad čest dođe do visine LFC na kojoj joj je gustoća jednaka gustoći okolnog zraka, tj. temperatura jednaka temepraturi okoliša (točka C), daljnje podizanje uzrokovati će neravnotežu između sile teže i sile gradijenta tlaka. Zbog toga će se čest, koja je sada toplija (rjeđa) od okoliša, dalje akcelerirati prema gore zbog uzgona. Konvekcija se od točke C dalje nastavlja slobodno (dok je duž krivulja AB i BC bila prisilna, jer je čest uvijek bila hladnija od okolnog zraka). Dakle, u točki C latentna nestabilnost prešla je u stvarnu (manifestnu) nestabilnost. Da bi se to dogodilo, potreban je:
1. dovoljno jak mehanički poticaj na dizanje, takav da se nadvlada stabilnost u donjem sloju, odnosno energiju inhibicije konvekcije CIN (vidi sliku) – drugim riječima, prisilno dizanje mora postojati i nakon postizanja zasićenja u točki B;
2. količina vodene pare u česti mora biti dovoljno velika tako da čest može relativno brzo postati zasićena.
Kako se čest nakon točke C nastavlja slobodno dizati, količina vodene pare u njoj se smanjuje, jer se para kondenzira. U točki D čest više nema vodene pare. Temperatura česti tu opet postaje jednaka temperaturi okolnog zraka, a slobodna konvekcija prestaje.
U slučajevima u kojima je poticaj dovoljno jak da dovede čest do kondenzacijske razine, formiraju se oblaci, čija je donja baza na visini zk, a ako je podizanje dovoljno da dovede čest do razine slobodne konvekcije, oblaci se vertikalno protežu sve do ravnotežne razine LNB (točka D) na kojoj je uzgon jednak nuli.
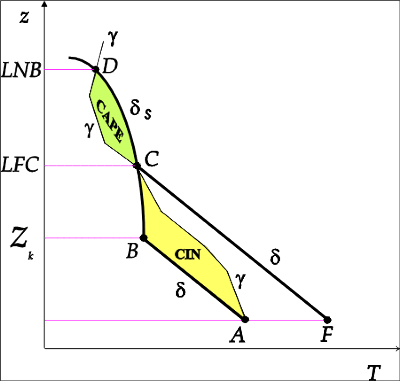
Slika 1. Ilustracija slobodne konvekcije. T je temperatura, a z visina. Vertikalni temperaturni gradijent g opisuje krivulju stanja atmosfere, d opisuje suhu adijabatu, a ds mokru adijabatu. A je početni položaj česti. U točki B čest se nalazi na kondenzacijskoj razini, u točki C je na razini slobodne konvekcije LFC. Nakon te visine postaje toplija od okolnog zraka, odnosno nestabilna u odnosu na okoliš. Točka D je na ravnotežnoj razini LNB, na kojoj više nema uzgona, a temperatura česti ponovno se izjednačava s temperaturom okolnog zraka. Iznad visine LNB čest je hladnija od okoliša (stabilna u odnosu na okoliš). Površina između točaka C i D, koja je omeđena mokrom adijabatom ds i krivuljom stanja g, odgovara konvekcijskoj raspoloživoj potencijalnoj energiji (CAPE), a površina između točaka A i C, koja je omeđena krivuljama suhom adijabatom d i krivuljom stanja g, energiji inhibicije konvekcije (CIN).
Vidi konvekciju i statičku (konvekcijsku) stabilnost.
Sloj miješanja
- atmosferski granični sloj u kojem je turbulencija veoma razvijena. Zbog razvijene turbulencije veličine poput potencijalne temperature, brzine vjetra, impulsa i koncentracije onečišćujuće tvari dobro su izmiješane, naročito u vertikalnom smjeru. Sloj miješanja obično postoji danju ljeti nad kopnom pri anticiklonalnim vremenskim uvjetima. Tada je generiran uzgonom i obično je statički nestabilan. Debljina mu tijekom dana raste te postiže maksimalnu vrijednost (~ 1 km) u posljepodnevnim satima, a također je i prostorno varijabilna.Vidi - struktura atmosfere, turbulencija, statička stabilnost.
Smicanje
- promjena vektorskog polja u određenom smjeru. U atmosferi je važno smicanje vektora vjetra, odnosno njegovih komponenata. Veliko smicanje postoji npr. u mlaznoj struji.Smorac
- dnevna grana obalne cirkulacije, pri tlu puše od mora prema kopnu.Specifična plinska konstanta (R)
- konstanta idealnog plina koja ovisi o molekularnoj masi plina MR = R*/M (J kg-1 K-1),
gdje je R* univerzalna plinska konstanta.
Za suhi zrak R = Rd = 287.0 J kg-1 K-1.
Za vodenu paru R = Rv = 461.5 J kg-1 K-1.
Za vlažan zrak specifična plinska konstanta ovisi o količini vodene pare u zraku
R = Rm = (Rvr+Rd)/(1+r)
![]() Rd(1+0.605 r),
Rd(1+0.605 r),
gdje je r omjer miješanja.
U jednadžbama termodinamike vlažnog zraka omjer specifičnih plinskih konstanti suhog zraka i vodene pare prikazujemo veličinom e:
e = Rv/Rd
gdje je e = 0.622.
Vidi univerzalna plinska konstanta, jednadžba stanja idealnog plina.
Specifična toplina (specifični toplinski kapacitet, c)
- toplina koju treba dodati jediničnoj masi da temperatura poraste za 1 K:c = đq/dT,
gdje je đq toplina dodana nekim općim procesom jedinici mase, a dT je promjena temperature. Specifična toplina ovisi o promatranoj tvari i općenito varira s temperaturom.
U meteorologiji nas zanimaju vrijednosti specifične topline zraka (koji je smjesa plinova) pri različitim teorijskim procesima (adijabatskom, izotermom, izobarnom i izosternom). Kako su varijacije specifične topline zraka s temperaturom male za raspon atmosferskih temperatura, najčešće ih zanemarujemo.
ADIJABATSKI PROCES
đq = 0, c = 0
IZOTERMNI PROCES
dT = 0, c → beskonačno
IZOBARNI PROCES
c = cp = (đq/dT)p = konst, gdje je
za suhi zrak cp = cpd = 1004.67 J kg-1 K-1 (pri 298.15 K);
za vodenu paru cp = cpv = 1865.1 J kg-1 K-1 (pri 298.15 K);
za vlažan zrak specifična toplina pri konstantnom tlaku ovisi o količini vodene pare u zraku
cp = cpm = (cpd+cpvr)/(1+r)
![]() cpd (1+0.8 r), gdje je r omjer miješanja.
cpd (1+0.8 r), gdje je r omjer miješanja.
IZOSTERNI / IZOPIKNI PROCES
c = cv = (đq /dT)a = konst, gdje je
za suhi zrak cv = cvd = 717.63 J kg-1 K-1;
za vodenu paru cv = cvv = 1403.2 J kg-1 K-1 (pri 298.15 K);
za vlažan zrak specifična toplina pri konstantnom tlaku ovisi o količini vodene pare u zraku
cv = cvm = (cvd+cvvr)/(1+r)
![]() cvd (1+0.9 r), gdje je r omjer miješanja.
cvd (1+0.9 r), gdje je r omjer miješanja.
U atmosferi se osim smjese plinova može nalaći i tekuća voda i/ili kristali leda. Stoga nas zanima i specifična toplina vode i leda. Za tekuću vodu specifična toplina se pri temperaturama većim od 0oC malo mijenja s temperaturom, pa možemo koristiti konstantnu vrijednost c = cl = 4185.5 J kg-1 K-1. Pri nižim temperaturama te varijacije su veće, pa tada za cl treba koristiti neke od empiričkih izraza (vidi npr. Jacobson, 1999). Specifična toplina leda za temperature u rasponu -40 0oC ≤ t < 0oC može se odrediti iz empiričkog izraza c = ci = 2104.6 + 7.322 t, gdje je t temperatura u Celzijevim stupnjevima.
• Jacobson, M.Z., 1999: Fundamentals of atmospheric modeling. Cambridge University Press, New York, 656.
Specifična vlažnost (q)
- omjer mase vodene pare mv i mase vlažnog zraka mm, gdje je mm = mv+md, a md je masa suhog zraka:Prikažemo li masu kao umnožak gustoće r i volumena V te zatim prikažemo gustoću vodene pare rv i suhog zraka rd pomoću jednadžbe stanja idealnog plina, dobivamo:
q = rvV/(rvV+rdV) = (e/RvT)/[e/(RvT)+(p-e)/(RdT)] = ee/(ee+p–e) = ee/[p–e(1-e)],
gdje su Rv i Rd specifične plinske konstante za vodenu paru i suhi zrak, e = Rd/Rv, p je tlak vlažnog zraka p = pd+e (vidi Daltonov zakon), a pd i e su tlakovi suhog zraka i vodene pare.
Ako je vlažan zrak zasićen vodenom parom (vidi relativnu vlažnost) specifična vlažnost jednaka je maksimalnoj specifičnoj vlažnosti qs
qs = ees/[p–es(1-e)],
gdje je es maksimalni (ravnotežni) tlak vodene pare.
Specifični volumen (a)
- volumen koji zauzima jedinična masa tvari a=V/m, gdje je V volumen a m masa promatrane tvari. Specifični volumen jednak je recipročnoj vrijednosti gustoće a=1/r.Spiralnost (H)
- skalarni produkt vektora brzine i vektora vrtložnosti:![]() ,
(m s-2)
,
(m s-2)
gdje je v vektor vjetra.
Katkad se promatra spiralnost u odnosu na oluju (H(c) ili SRH):
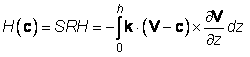 ,
(m2 s-2)
,
(m2 s-2)
gdje je V-c relativna brzina vjetra u odnosu na oluju, c je vektor gibanja oluje, V(z) je vektor vjetra u okolišu, k je jedinični vektor u smjeru vertikalne osi, a h je debljina promatranog sloja. Pozitivni SRH odgovara ciklonalnoj rotaciji.
Spiralnost se često koristi u istraživanjima tornada. Tada se najčešće određuje u sloju zraka od tla do
![]() 3 km, budući da se za taj sloj dobivaju najveće vrijednosti
SRH. U novije vrijeme u nekim studijama koristi se i spiralnost u prvom kilometru atmosfere.
3 km, budući da se za taj sloj dobivaju najveće vrijednosti
SRH. U novije vrijeme u nekim studijama koristi se i spiralnost u prvom kilometru atmosfere.
SRH je usko povezana s nastankom superćelija do čega može doći ako hodograf pokazuje zakretanje vjetra s visinom u smjeru kazaljke na satu, a da se pri tom vektror gibanja oluje nalazi udesno od hodografa.
Srednji radijus Zemlje
- Rz = 6371 km. Zbog spljoštenosti Zemlje (vidi silu težu), ekvatorijalni radijus je oko 21 km veći od polarnog.Stacionarno strujanje
- ono koje se ne mijenja u vremenu.Standardni uvjeti
- uvjeti pri kojima je tlak p = 1013.250 hPa, a temperatura T = 273.15 K. Pri standardnim uvjetima volumen jednog kilomola plina mora biti jednak molarnom volumenu Vm = 22.414 m3 kmol-1, bez obzira na to koji plin promatramo.Vidi molarni volumen, Avogadrov broj.
Statička (konvekcijska) stabilnost
- stanje atmosfere o kojem ovisi da li će se čest pomaknuta adijabatski u vis vratiti u početni položaj (stabilno stanje), ostati u novom položaju (indiferentno ili neutralno stanje), ili će se nastaviti gibati prema gore (nestabilno stanje). U statički stabilnoj atmosferi čest je u novom položaju gušća (hladnija) od okolnog zraka, u neutralnoj atmosferi čest u novom položaju ima jednaku gustoću (i temperaturu) kao i okolni zrak, dok je u statički nestabilnoj atmosferi čest toplija (rjeđa) od okolnog zraka.Atmosfera može biti apsolutno stabilna, uvjetno nestabilna, apsolutno nestabilna ili neutralna (indiferentna) (vidi sliku).
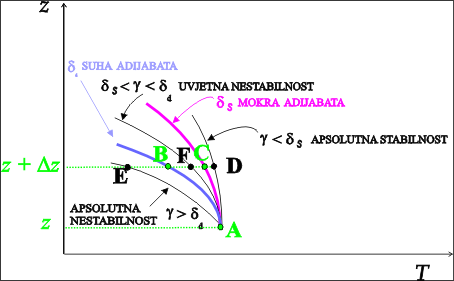
Čest se najprije nalazi u točki A na visini z, gdje ima temperaturu T koja je u toj točki jednaka temperaturi okolnog zraka. Pomakne li se čest adijabatskim procesom na visinu z+Dz, zbog adijabatskog ohlađivanja temperatura će joj se sniziti na T–dDz, gdje je d adijabatska stopa ohlađivanja. Ako je čest u točki A bila nezasićena vodenom parom, tada će do visine z+Dz 'putovati' po suhoj adijabati, odnosno ohlađivati će se suhoadijabatskom stopom dd te će na visini z+Dz (točka B) imati temperaturu T– ddDz. Međutim, ako je čest u točki A bila zasićena, pri dizanju će se ohlađivati mokroadijabatskom stopom δs. Stoga će na visini z+Dz (točka C) imati temperaturu T – dsDz. Daljnje ponašanje česti ovisiti će o statičkoj stabilnosti atmosfere, odnosno o međusobnom vertikalnog temperaturnog gradijenta g i adijabatske stope:
- Ako je g<ds, okolni zrak na visini z+Dz (točka D) topliji je od česti, bez obzira da li je čest zasićena (točka C) ili nezasićena (točka B) - atmosfera je statički apsolutno stabilna. Stoga će se čest koja je hladnija (gušća) od okolnog zraka nastojati vratiti u početni položaj.
- Ako je ds<g <dd, okolni zrak na visini z+Dz (točka F) topliji je od nezasićene česti (točka B), ali je hladniji od zasićenje česti (točka C) - atmosfera je statički uvjetno nestabilna, tj. stabilna za nezasićenu, a nestabilna za zasićenu čest. Prema tome nezasićena (hladnija, tj. gušća) čest vraćati će se prema početnom položaju, a zasićena (toplija, tj. rjeđa od okolnog zraka) nastaviti će se gibati u vis.
- Ako je g>dd, čest je na visini z+Dz toplija (rjeđa) od okolnog zraka, bez obzira na njenu zasićenost - atmosfera je statički apsolutno nestabilna te se čest dalje nastavlja gibati u vis.
- Ako je g=dd, atmosfera je statički neutralna za suhu čest, dok je za zasićenu čest nestabilna. Nadalje, ako je g=ds, atmosfera je neutralna za zasićenu čest, dok je za nezasićenu čest stabilna.
Statičku (konvekcijsku) stabilnost atmosfere možemo odrediti na temelju promjene potencijalne temperature q s visinom ili iz vrijednosti Richardsonovog broja Ri:
| stabilna | neutralna (indiferentna) | nestabilna | |
|
|
> 0 | = 0 | < 0 |
| Ri | > 0 | = 0 | < 0 |
Pri tom za suhu atmosferu koristimo potencijalnu temperature suhog zraka qd:
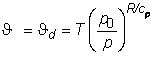
dok za vlažan zrak gledamo promjenu ekvivalentne potencijalne temperature qe,a s visinom.
Vidi potencijalnu nestabilnost i dinamičku nestabilnost.
Stratificirani fluid
- fluid čija gustoća varira u smjeru sile teže. Pod stratificiranim fluidom obično podrazumjevamo fluid kojem gustoća opada s visinom, odnosno fluid koji je statički stabilan.Stratokumulus (Stratocumulus, Sc)
- u nas česti niski oblak. Obično ne daje oborinu. Javlja se u niskim slojevima sastavljenim od znatnog broja grudastih oblaka skupljenih u grupe koji mogu ili ne moraju biti međusobno slijepljeni. Oblaci u sloju mogu biti poredani u valove, brazde, pruge i redove. Rubovi pojedinih oblaka su tanji, propuštaju svjetlost i bijeli su, a sredina im je deblja i tamnija. Prividna širina pojedinog oblaka, ako se nalazi bar 30o nad horizontom, je veća od 5o. Od altokumulusa ga tada možemo razlikovati po tome što oblak ne možemo prekriti s sa tri skupljena prsta, a od kumulusa po tamnijoj boji. Stratokumulus spada u vodene oblake, premda ponekad može imati i ledenih elemenata.

Stratokumulusi nad Zagrebom 11. travnja 2005. (Snimila Z. Bencetić Klaić).

Stratokumulusi nad Splitom. (Snimila Lj. Vilibić).
Stratopauza
- vidi strukturu atmosfere.Stratosfera
- vidi strukturu atmosfere.Stratus (Sc)
- niski slojeviti oblak jednolične i neizražene podnice. Može dati slabu oborinu o obliku rosulje, zrnatog snijega, ili kad je jako hladno, ledenih iglica. Ako nije predebeo, kroz njega se može vidjeti Sunce kao žućkastu ploču. Dno stratusa ne mora biti ravno već može biti iskidano i čupavo. Manji oblačni elementi čupavog oblika nazivaju se stratusi fractusi. St fractus se često može vidjeti ispod baze drugih oblaka. Stratus može ohlađivanjem prizemnog sloja zraka zbog 1) dugovalnog zračenja tla (npr. noću ili zimi); ili 2) advekcije toplog zraka nad hladnu podlogu. Ako se stratus nalazi pri tlu nazivamo ga maglom.Strujnica
- krivulja čija je tangenta u bilo kojoj točki paralelna s trenutnom brzinom fluida u toj točki. Kod geostrofičkog strujanja strujnice su paralelne s izobarama odnosno izohipsama apsolutne topografije.Struktura atmosfere
- podjela atmosfere po slojevima. U meterologiji je uobičajena podjela atmosfere na temelju promjene temperature s visinom (vidi sliku).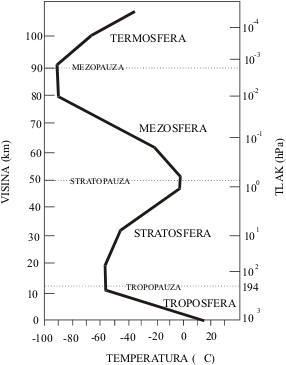
Prosječna promjena temperature visinom u prvih stotinjak km atmosfere.
Troposfera je najdonji dio atmosfere. Troposfera se najvećim dijelom zagrijava se od Zemljine površine - apsorpcijom Zemljinog dugovalnog zračenja te turbulentnim dotokom senzitivne i latentne topline sa Zemljine površine. Stoga u troposferi temperatura naglo opada s visinom (u prosjeku oko 0.65oC/100 m). Prosječna temperatura na vrhu troposfere je približno -60oC.
Premda je troposfera najtanja, u njoj se nalazi oko 80 % mase cijele atmosfere. Nadalje, u troposferi se događaju gotovo svi procesi i pojave koji utječu na vrijeme (poput vremenskih fronti, uragana, oluja, oblaka, nastajanja oborine i drugog), te se u njoj nalazi gotovo sva atmosferska vodena para. Troposfera je deblja nad ekvatorijalnim područjem (od 16 do 18 km), dok je nad polarnim područjem tanja (od 7 do 9 km).
Kako se u troposferi hladniji zrak nalazi iznad toplijeg, to dovodi do vertikalnih gibanja i miješanja zraka iz različitih slojeva, budući da troposfera, poput svih sustava u prirodi, teži k postizanju ravnotežnog stanja. Međutim, to ravnotežno stanje, nikad se ne postiže, budući da radijacija Sunca neprestano traje, te na taj način neprestano podržava postojanje vertikalnih temperaturnih gradijenata.
Najdonji dio troposfere naziva se atmosferski granični sloj. Atmosferski granični sloj debeo je, ovisno o uvjetima, od nekoliko stotima metara do 3 km, a karakterizira ga izrazita turbulencija. Taj sloj je u direktnom dodiru sa Zemljinom površinom, koja na njega utječe na različite načine: evapotranspiracijom, emisijom onečišćujućih tvari, antropogenom emisijom topline, trenjem, modificiranjem strujanja zbog postojeće topografije i drugim. Atmosferski granični sloj vrlo brzo (na vremenskoj skali ~ 1 h) reagira na utjecaje Zemljine površine. Ostatak troposfere, koji se naziva slobodna troposfera, također reagira na utjecaje Zemljine površine, ali je njegova reakcija, puno sporija (~ 1 dan).
Vrh troposfere naziva se tropopauza i u prosjeku se u umjerenim širinama nalazi na visinama od 11 do 12 km nad morskom razinom. Temperatura je u tropopauzi približno konstantna s visinom. Tropopauza je najhladnija nad tropima, gdje temperatura može biti i niža od -70ºC, dok je najtoplija nad polovima, gdje se katkad izmjeri i -40ºC. Tropopauza nije uvijek kontinuirana. Često je u tropima odijeljenja, tako da se na širinama oko 30o lomi, a nova tropopauza se formira na manjoj visini. Taj niži dio tropopauze nagnut je prema polu i katkad, protežući se do pola, može imati još jedan diskontinuitet. U blizini diskontinuiteta tropopauze često se nalazi mlazna struja.
Stratosfera se nalazi iznad tropopauze. Temperatura u stratosferi raste visinom zbog prisustva ozona, koji apsorbira UV zračenje i pri tom je zagrijava. Zagrijavanje je jače u gornjem dijelu statosfere u kojem ima i više UV zračenja i dovoljno ozona. U skladu s tim temperatura brže raste visinom u gornjem dijelu stratosfere, pa su tamo temperature katkad visoke poput onih pri tlu.
Kako se u stratosferi topliji zrak nalazi iznad hladnijeg, vertikalna gibanja su prigušena. Time je onemogućeno vertikalno miješanje zraka (izuzev nevelike razmjene s troposferom duž tropopauze). Stoga tvar koja dospije u stratosferu može u njoj ostati jako dugo. Tako npr. čestice koje dospiju u stratosferu prilikom vulkanskih erupcija mogu u njoj ostati nekoliko godina. Vrh stratosfere naziva se stratopauza, a nalazi se na visini od oko 50 km nad Zemljinom površinom. U stratopauzi je temperatura približno konstantna s visinom.
Iznad stratopauze nalazi se svega oko 0.1 % mase atmosfere. Od toga se oko 99 % mase nalazi u mezosferi, koja se proteže na visinama od oko 50 do oko 80 km nad tlom. U mezosferi, koja se još naziva i srednja atmosfera, ima vrlo malo ozona, kisika i dušika, koji bi mogli u znatnijoj količini apsorbirati Sunčevo zračenje. Stoga temperatura opada s visinom, budući da mezosfera gubi toplinu zračenjem, prvenstveno ugljikovog dioksida. Sastojci u gornjem dijelu mezosfere u velikoj mjeri su ionizirani. Na vrhu mezosfere, koji nazivamo mezopauza, temperatura opada i do -90oC. Duž mezopauze, koja se nalazi na visinama od oko 85 do 90 km, temperatura je konstantna s visinom.
Iznad mezopauze nalazi se termosfera. U tom sloju temperatura opet počinje rasti s visinom. Temperatura u termosferi raste zbog toga što plinovi u njoj potpuno apsorbiraju Sunčevo UV zračenje vrlo kratkih valnih duljina. Nadalje, u termosferi se nalazi mnogo ioniziranih atoma i molekula, pa taj dio atmosfere zajedno s gornjim dijelom mezosfere čini ionosferu.
Vrh termosfere, termopauza, nije dobro definiran. Procjenjuje se da se nalazi na visinama između 500 i 1000 km, te da se jako mijenja u ovisnosti o Sunčevom zračenju. Temperatura u termopauzi također nije dovoljno istražena, a prema nekim studijama katkad je veća i od 2000oC.
Sublimacija
- proces direktne promjene faze iz krutog u plinovito stanje, bez taljenja.Vidi latentna toplina, isparavanje, kondenzacija, Clausius-Clapeyronova jednadžba.
Sunčevo zračenje
- ukupno elektromagnetsko zračenje koje emitira Sunce. Sunčevo zrači približno poput crnog tijela čija je temperatura oko 5700 K. Oko 99.9 % energije Sunčevog zračenja otpada na male valne duljine (od 0.15 do 4.0 mm, uz maksimalni intenzitet pri približno 0.5 mm), stoga Sunce zrači kratkovalno. Oko pola ukupne energije Sunčevog zračenja nalazi se u vidljivom dijelu spektra, a ostatak većinom u rasponu od 0.75 do približno mm (tj. na rubu toplinskog dijela spektra). Tek mali dio leži u ultraljubičastom dijelu spektra.Sunčevo zračenje koje dopre do tla zovemo globalno kratkovalno Sunčevo zračenje.
Vidi direktno zračenje, difuzno zračenje, radijacijsko-apsorpcijska svojstva sustava Zemlje i atmosfere.
Superćelija
- oluja koju je karakteriziraju perzistentne mezoskalne rotirajuće uzlazne struje koje nazivamo mezociklonama. Proteže se visoko u odnosu na gornju bazu kumulonimbusa (koja je obično na visini od 8 do 15 km). Superćelija živi i do 6 sati i može producirati sve tipove ekstremnog vremena popraćenog štetama: od velike tuče, čestih munja koje dopiru do tla, naglih poplava, razornih vjetrova, pa do tornada. Većina jakih i razornih tornada nastaje u superćelijama. Područja uzlaznih i silaznih struja u superćeliji horizontalno su odijeljena, stoga takva oluja traje dulje od obične. Superćelije nastaju u produčjima u kojima su vertikalno smicanje vjetra i nestabilnost veliki.Jedno od najvažnijih svojstava superćelije je perzistentna pozitivna ili negativna korelacija između vertikalne brzine i vertikalne komponente relativne vrtložnosti. Drugim riječima, najkarakterističnije strujanje zraka u superćeliji je duboka i perzistentna mezociklona.
Vjerojatnost da nastupi superćelijska oluja može se procjeniti pomoću više parametara poput konvekcijske raspoložive potencijalne energije CAPE, bulk-Richardsonovog broja (link Richardsonov broj) RiB, spiralnosti u odnosu na oluju SRH i EHI indeksa.
Supsidencija
- lagano spuštanje zraka nad većim područjem. Zrak se pri spuštanju, zbog dolaska na veći tlak adijabatski komprimira i pri tom zagrijava. Zbog supsidencije strujanje pri tlu divergira. U visini silazna strujanja moraju (zbog sačuvanja mase) biti kompenzirana konvergencijom zraka. Supsidencija postoji na primjer u anticikloni.