POJMOVNIK - R

Radijacijsko-apsorpcijska svojstva Zemlje i atmosfere

- Zračenje Sunca je kratkovalno, a Zemlje dugovalno (vidi sliku 1). Slika 1 pokazuje da atmosferski sastojci puno efikasnije apsorbiraju (link apsorpcija) dugovalno (Zemljino) od kratkovalnog (Sunčevog) zračenja. Atmosfera zbog apsorpcije zračenja i sama dugovalno zrači. To zračenje nazivamo protuzračenje atmosfere.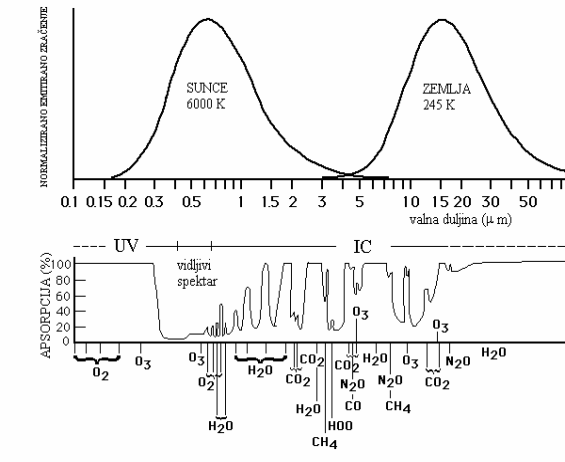

Slika 1. Normalizirano emitirano zračenje Sunca pri temperaturi površine od 6000 K i Zemlje pri temperaturi površine od 245 K u ovisnosti o valnoj duljini (gore), te apsorpcijska svojstva atmosferskih sastojaka (dolje) (prema Schneider, 1996).

Od kratkovalnog zračenja Sunca koje dođe na vrh atmosfere, u prosjeku se samo oko dvadesetak posto apsorbira u atmosferi i oblacima (vidi sliku 2), oko 30 % se zbog raspršenja i refleksije gubi u svemir, a preostalih 50 % dolazi do Zemljine površine, te tamo biva apsorbirano. Zemljina površina dio tog apsorbiranog zračenja dalje utroši na vlastito toplinsko zračenje te na senzitivnu i latentnu toplinu, koje se turbulentnim tokovima prenose u atmosferu. Najveći dio energije koju Zemlja gubi dugovalnim zračenjem i turbulentnim tokovima topline apsorbira se u samoj atmosferi.

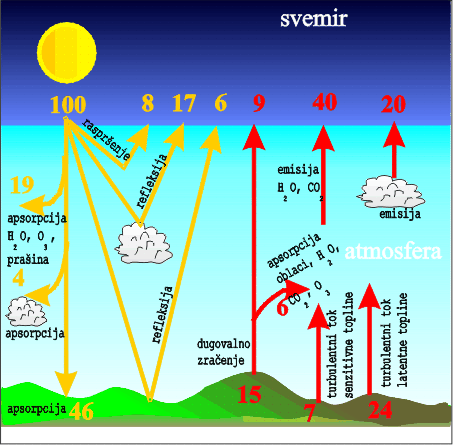
Slika 2. Bilanca zračenja u sustavu Zemlja-atmosfera. Slika prikazuje prosječno stanje tijekom višegodišnjeg razdoblja. (U različitim izvorima mogu naći nešto drugačije vrijednosti pojedinačnih komponenti bilance, ovisno o tome na koje razdoblje se odnose.) Potrebno je uočiti da je neto dobitak/gubitak energije gledan zasebno na vrhu atmosfere (100-8-17-6-9-40-20) jednak nuli. Slično vrijedi i u samoj atmosferi (19+4+6+7+24-40-20=0), te na Zemljinoj površini (46-15-7-24=0). To znači da je sustav Zemlja-atmosfera, ako ga promatramo tijekom duljeg razdoblja, u energijskoj ravnoteži. U ravnoteži su također i njegovi pojedini dijelovi (Zemljina površina, atmosfera i vrh atmosfere). Kada ne bi bilo tako, sustav bi se s vremenom ili ohlađivao ili zagrijavao. Promatramo li sustav tijekom kraćeg razdoblja (npr. nekoliko dana ili mjeseci), pojedini dijelovi sustava, kao i sustav u cjelini, mogu dobivati ili gubiti energiju.

Radijacijsko-apsorpcijska svojstva sustava Zemlja-atmosfera direktno utječu na strukturu atmosfere.

Vidi sastav atmosfere, struktura atmosfere.

Schneider S.H., (urednik), 1996: Encyclopedia of Climate and Weather, Oxford University Press, Oxford, 929 str.

Radijacijsko hlađenje (noćno hlađenje)

- snižavanje temperature Zemljine površine i zraka uz nju. Događa se noću kada je bilanca zračenja na Zemljinoj površini negativna, odnosno kada je energija koju Zemljina površina izgubi zbog dugovalnog zračenja veća od energije koju primi protuzračenjem atmosfere. Radijacijsko hlađenje najjače je za vedrih, suhih i tihih noći te su tada jutra hladna.

Razina bez uzgona (ravnotežna razina, LNB)

- visina na kojoj prestaje slobodna konvekcija jer se temperatura česti ponovo izjednači s temperaturom okolnog zraka. Na toj visini uzgon je jednak nuli.

Vidi: slobodna konvekcija, uzgon.

Razina slobodne konvekcije (LFC)

- razina na kojoj čest zraka nakon prisilnog dizanja postaje toplija od okolnog zraka te se dalje nastavlja dizati bez prisile. Niske vrijednosti LFC pogoduju nastanku mezociklona.

Vidi slobodnu konvekciju, statičku stabilnost i mezociklonu.

Relativna topografija

- polje razlike geopotencijala (link geopotencijal) između dvije izobarne plohe (vidi sliku 1). Na gornjoj plohi tlak je p₂, a na donjoj p₁, relativna topografija RT p₂/p₁ jednaka apsolutnoj topografiji plohe p₂ umanjenoj za apsolutnu topografiju plohe p₁. Polje relativne topografije određuje se na temelju podataka dobivenih visinskim radiosondažnim mjerenjima.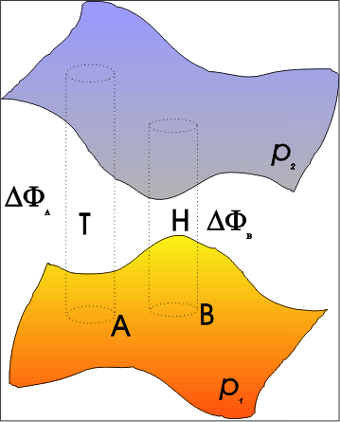

Slika 1. Slika prikazuje izobarne plohe (link izobarna ploha) p2 i p1. Kako je u stupcu A zrak topliji (rjeđi) nego u stupcu B, to su u tom području izobarne plohe međusobno udaljenije. (U rjeđem zraku tlak se sporije mijenja s visinom nego u gušćem zraku. Tako npr. da bi izmjerili promjenu tlaka od -1 hPa, moramo se u toplom zraku više penjati u vis nego u hladnom.) Stoga je i razlika geopotencijala Df = f(p₂)-f(p₁) u području A veća nego u području B: Df_A > Df_B.

Prikažemo li polje razlike geopotencijala na karti, dobivamo relativnu topografiju RT p₂/p₁. U meteorologiji je uobičajeno analizirati relativnu topografiju izobarnih ploha 500/1000 hPa. Jedan primjer RT 500/1000 hPa prikazan je na slici 2.

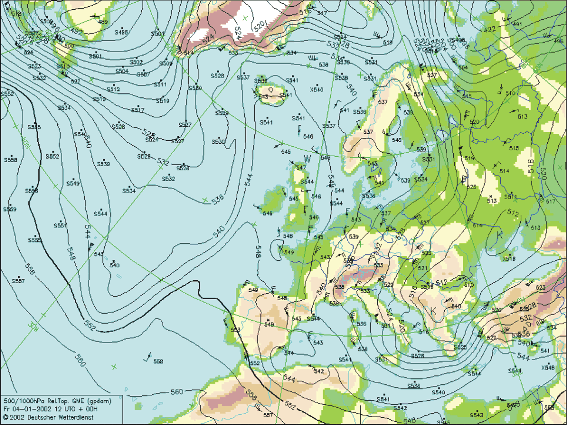
Slika 2. . Relativna topografija RT 500/1000 hPa nad Europom 4. siječnja 2002. u 12 UTC (13 SEV). Osim izolinija Df, koje su prikazane u geopotencijalnim dekametrima, na karti se vidi i polje vjetra na 500 hPa plohi. (Polje vjetra prikazuje se na isti način kao i na visinskim kartama – vidi sliku 3 u apsolutnoj topografiji). U ovom primjeru uočava se područje hladnog zraka sa središtem u jugoistočnoj Europi, gde je razlika geopotencijala manja od 512 gpdkm. Južno od središta hladnog zraka (jug Italije i Grčke te zapadna Turska) horizontalni gradijenti temperature su izrazito veliki. Istovremeno, na istočnom rubu Atlantika nalazi se topao zrak. Tako se npr. Britansko otočje nalazi u području visokih vrijednosti RT koje su u rasponu od 544 do 548 gpdkm.

Polje relativne topografije usko je povezano sa poljem temperature (vidi sliku 1), odnosno s postojanjem horizontalnih gradijenata temperature koji su pak u vezi s poljem strujanja. Ako se temperatura zraka duž horizontalne ravnine mijenja, to znači da se u promatranom području i geostrofički vjetar mijenja s visinom. Drugim riječima, tamo gdje postoje horizontalni gradijenti razlike geopotencijala Df (odnosno horizontalni gradijenti temperature), postoji i termalni vjetar.

Relativna vlažnost (u)

- omjer stvarnog r i maksimalnog (ravnotežnog) omjera miješanja (omjer miješanja) vodene pare r_s izražen u postocima:

u = 100 r/r_s (%),

Uvrstimo li u jednadžbu izraze za omjere miješanja r = ee/(p–e) i r_s = ee_s/(p–e_s), dobivamo

u = 100 (e/e_s)(p –e_s)/(p –e) (%).

Kako je (p –e_s) /(p –e) 1 (jer je p puno veći i od e i od e_s), to se u meteorološkoj praksi koristi izraz

u = 100 e/e_s (%),

gdje su e i e_s, stvarni i maksimalni tlak vodene pare, koji se za razliku od r i r_s mogu odrediti na temelju rutinskih meteoroloških mjerenja.

U stanju zasićenja zraka vodenom parom u = 100 %.

Vidi Clausius-Clapeyronovu jednadžbu.

Rendgensko zračenje (x-zrake)

- elektromagnetsko zračenje valnih duljina manjih od 200 nm, a većih od valnih duljina g-zraka.

Vidi radijacijsko-apsorpcijska svojstva sustava Zemlja-atmosfera.

Richardsonov broj (R_i)

- bezdimenzijski parametar za ocjenu dinamičke stabilnosti zračne struje u kojoj postoji vertikalno smicanje horizontalne brzine (koje je dinamički faktor) i vertikalni gradijent potencijalne temperature q (koje je uzgonski faktor). R_i je omjer uzgona i sile inercije:

gdje je N Brunt-Väisälaä frekvencija. U gornjem izrazu i statičku stabilnost Mq /Mz i smicanje vjetra Mu/Mz treba računati lokalno (u točki).

Vrijednost Richardsonovog broja ukazuje na to da li je konvekcija slobodna (veliki R_i, što drugim riječima znači da je uzgon veći od sile inercije) ili prisilna (R_i << 1, sila inercije dominira nad uzgonom).

Kako u praksi ne raspolažemo s podacima o lokalnim gradijentima Mq /Mz i Mu/Mz, aproksimiramo ih konačnim razlikama. Tako dobivamo približnu vrijednost Richardsonovog broja tzv. bulk-Richardsonov broj:

koji se najčešće upotrabljava u meteorologiji. Pri tom je

Dq = q₂ – q₁; Dz = z₂ – z₁; Du = u₂ – u₁; Dv = v₂ – v₁,

gdje se vrijednosti s indeksom 1 i 2 odnose na dno i vrh promatranog sloja čija je debljina Dz.

Kod proučavanja tornada (link tornado) bulk-Richardsonov broj se računa iz:

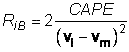
gdje su v_l i v_m vektori vjetra u donjoj (indeks l) i srednjoj (indeks m) troposferi, a CAPE je konvekcijska raspoloživa potencijalna energija.

Vidi dinamička nestabilnost.

Rosište (T_d)

- temperatura na kojoj čest zraka izobarnim ohlađivanjem postaje zasićena vodenom parom. Ako se zrak izobarno ohladi do temperature rosišta (to se npr. može dogoditi noću zbog radijacijskog hlađenja, tada će se na tlu pojaviti rosa (T_d > 0^oC) ili mraz (T_d ≤ 0^oC).

Rosište možemo odrediti grafički pomoću termodinamičkog dijagrama (vidi sliku 1), ili ga možemo izračunati pomoću integralnog oblika Clausius-Clapeyronove jednadžbe:

(1)

gdje je e_s(T) ravnotežni tlak vodene pare pri temperaturi T, e_s0 je ravnotežni tlak pri temperaturi T₀ = 273.15 K (e_s0 = 6.11 hPa), L_lv je latentna toplina isparavanja/kondenzacije, a R_v je specifična plinska konstanta vodene pare. U jednadžbu (1) uvrstimo uvjet da je stvarni tlak vodene pare na početnoj temperaturi T jednak maksimalnom (ravnotežnom) tlaku vodene pare na temperaturi rosišta:

e(T) = e_s(T_d).

Tako dobivamo:

(2)

te iz poznatog tlaka vodene pare e(T) možemo izračunati rosište T_d.

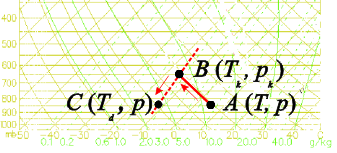
Slika 1. Grafičko određivanje rosišta T_d pomoću kosog emagrama. Čest se u početku nalazi na tlaku p i temperaturi T (točka A) te ima omjer miješanja r = r(T). Čest se izobarno hladi (p = konst) do temperature T_d (točka C) na kojoj je postojeći omjer miješanja r(T) jednak maksimalnom omjeru miješanja pri temperaturi T_d: r(T) = r_s(T_d ). Do rosišta možemo doći tako da idemo po suhoj adijabati od početne točke A pa do kondenzacijske razine (točka B) koja se nalazi na temperaturi T_k i tlaku p_k. Zatim se od točke B spuštamo spuštamo po izoliniji maksimalnog omjera miješanja sve dok ne dođemo do početnog tlaka p. Rosište se nalazi u točki C koja je sjecište izobare p i krivulje maksimalnog omjera miješanja koja prolazi kroz točku B.

Rossbyjev broj

- omjer magnitude horizontalne akceleracije i horizontalne komponente akceleracije zbog Coriolisove sile:

Ro = U / L f₀

gdje je U skala horizontalne brzine, L je horizontalna skala duljine, a f₀ skala Coriolisovog parametra (f₀ = 10^-4 s^-1). Što je Ro manji to je strujanje bliže geostrofičkom. (Vidi analizu skala).

Rossbyjev parametar (b)

- mjera promjene Coriolisovog parametra f duž meridijana:

gdje os y usmjerena prema sjeveru, W je kutna brzina rotacije Zemlje, f je geografska širina, a R_z je srednji radijus Zemlje.

Najčešće pretpostavljamo da je b konstantan. Rossbyjev parametar važan je za nastanak Rossbyjevih valova (link Rossbyjevi valovi).

Rossbyjevi valovi

- još ih nazivamo i planetarni ili dugi valovi. Valoviti barotropni poremećaji u polju strujanja u području prevladavajuće zapadne zonalne struje (tj. u ekstratropskim širinama). Vide se u srednjoj i gornjoj troposferi (vidi sliku 1), naročito na sjevernoj hemisferi. Valnih su duljina od oko 5000 do 10000 km. Zemlju opasuje oko tri do pet valova. Osnovni uzrok nastanka Rossbyjevih valova je promjena Coriolisovog parametra duž meridijana, a iniciraju ih veliki planinski lanci (poput Himalaje i Stijenjaka) zbog kojih zapadna zonalna struja počinje meandrirati.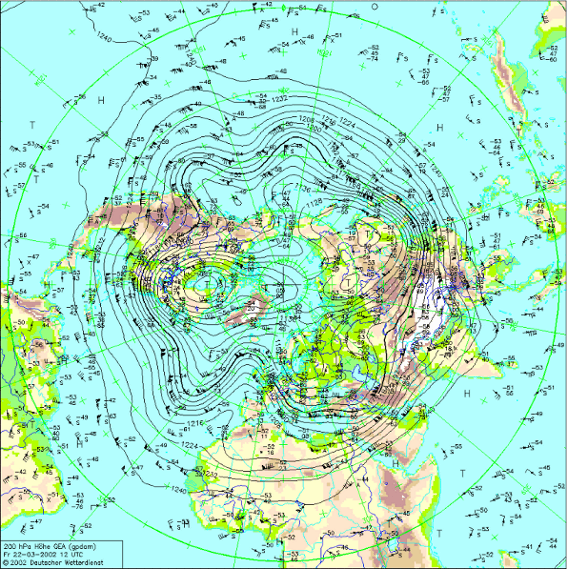

Slika 1. Rossbyjevi valovi na sjevernoj hemisferi 200 hPa izobarnoj plohi 22. ožujka 2002. Valovita poremećenja u polju strujanja (valovit oblik izolinija geopotencijala vide se u ekstratropskim zemljopisnim širinama.

Više o Rossbyjevim valovima možete saznati iz:

• Holton, J.R., 1992: Introduction to Dynamic Meteorology. Academic Press, third edition, London, 511 str.