POJMOVNIK - J
Jednadžba gibanja u prirodnom koordinatnom sustavu
Horizontalna brzina u prirodnom koordinatnom sustavu (link prirodni koordinatni sustav) je
vh = V t ,
gdje je s strujnica, a V = ds/dt. Prema tome, akceleracija je
dvh/dt = (dV/dt) t + V (dt/dt).
Vremenska promjena jediničnog vektora t koja prati gibanje je
dt/dt = (dt/ds) (ds/dt) = (dt/ds) V.
Kako je (vidi sliku 1) element strujnice ds = Rda, gdje je R radijus zakrivljenosti strujnice, to je
![]()
Sa slike je vidljivo da je d t usmjeren u smjeru n osi te da vrijedi razmjer
|d t| / d s = |t| / R,
odatle je
![]() .
.
Uvrstimo li gornji izraz u jednadžbu (2), dobivamo
dt/dt = (dt/ds)V = (V/R)n. (3)
Nakon uvrštavanja jednadžbe (3) u izraz za akceleraciju (1) dobivamo akceleraciju u obliku
dvh/dt = (dV/dt)t + (V2/R)n. (4)
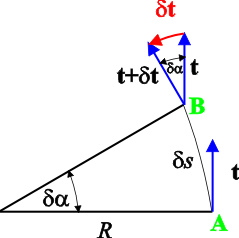
Slika 1. U točki A koja leži na strujnici s jedinični vektor u s smjeru je t, dok je u točki B, budući da je strujnica zakrivljena, jedinični vektor t+dt. Radijus zakrivljenosti strujnice je R. Strujnica leži u horizontalnoj ravnini.
Akceleracija česti prikazana jednadžbom (4) mora biti jednaka akceleraciji koja je rezultanta akceleracija svih sila koje djeluju na čest. Zanemarimo li trenje, na čest u horizontalnoj ravnini djeluju samo
Coriolisova sila i sila gradijenta tlaka.
U horizontalnoj ravnini (slika 2) Coriolisova akceleracija je FC =
-fVn, gdje je f Coriolisov parametar, a akceleracija sile gradijenta tlaka ima dvije komponente
![]() .
.
Uvrstimo li te dvije akceleracije u jednadžbu (4), dobivamo horizontalnu jednadžbu gibanja u prirodnom koordinatnom sustavu u vektorskom obliku
![]() ,
,
ili po komponentama
smjer s:
![]() ,
,
smjer n:
![]() .
.
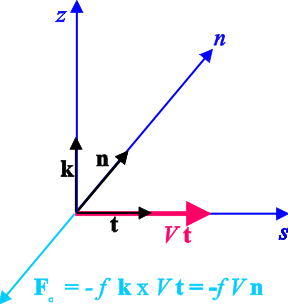
Slika 2. Horizontalna komponenta akceleracije Coriolisove sile Fc je orijentirana u negativnom smjeru osi n.
Jednadžba kontinuiteta (zakon sačuvanja mase)
- jedan od tri osnovna fizikalna zakona koji upravljaju gibanjima u atmosferi. (Preostala dva su zakon sačuvanja impulsa i zakon sačuvanja energije.) Zakon sačuvanja mase formalno prikazujemo jednadžbom kontinuiteta. Tu jednadžbu možemo izvesti na dva načina: Lagrangeovim i Eulerovim pristupom. U prvom pratimo promjene gustoće materijalne česti fluida unutar kontrolnog voulmena, koji je zbog strujanja fluida promjenjiv. Dakle, promjene pratimo prateći gibanje materijalnog elementa, odnosno u Lagrangeovom sustavu. Eulerovim pristupom promjene mase pratimo unutar fiksnog elementa volumena, odnosno pratimo ih u Eulerovom sustavu.
1. Lagrangeov način
Promatramo infinitezimalno mali materijalni element fluida fiksne mase dM, koji je u početnom trenutku pravokutan te zauzima volumen
dV = dxdydz. Materijalni element nalazi se u polju strujanja, te će se zbog toga nakon kratkog vremena deformirati (vidi sliku 1). Volumen će se zbog strujanja relativno promijeniti za iznos
![]() . (1)
. (1)
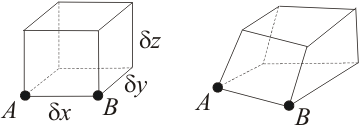
Slika 1. Materijalni element fluida, koji je u početku bio pravokutan (lijevo) deformira se zbog polja strujanja (desno).
Pogledajmo čemu je jednak prvi član s desne strane jednadžbe (1). Položaj točaka A i B nije funkcija prostora (x, y, z), već ovisi samo o vremenu t. Stoga je
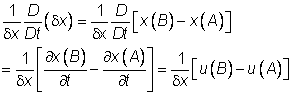 ,
,
gdje su u(B) i u(A) x-komponente brzine u točkama B i A. Budući da je dx infinitezimalno malen to je
![]() .
.
Slično dobivamo i za infinitezimalno male dy i dz
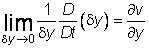 ,
,
![]() ,
,
gdje su v i w komponente brzine fluida u y i z smjeru. Odatle za
![]() jednadžba (1) prelazi u
jednadžba (1) prelazi u
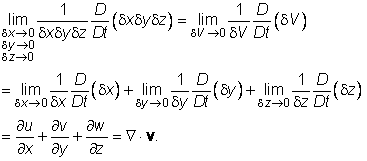
Budući da je dV = dM /r, gdje je r gustoća materijalnog elementa fluida, gornju jednadžbu možemo pisati ovako
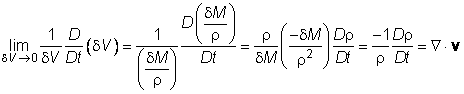 .
.
Tako dobivamo jednadžbu kontinuiteta
![]() , (2)
, (2)
gdje veličina
![]()
prikazuje divergenciju brzine, a Dr / Dt je totalni (Lagrangeov) diferencijal gustoće.
2. Eulerov način
Izvedimo sada jednadžbu kontinuiteta promatrajući fiksni (Eulerov) infinitezimalno mali element volumena koji se nalazi u polju strujanja (slika 2). Zbog strujanja fluida, u takav element volumena kontinuirano ulazi i iz njega kontinuirano izlazi neka masa fluida. Pogledajmo najprije neto dotok mase koji postoji samo zbog
x-komponente strujanja. Kroz lijevu plohu, čija je površina
dydz, u jedinici vremena u volumen uđe masa fluida
A = [ru – (dx/2)
![]() (ru)/
(ru)/![]() x]
dydz. Istovremeno, kroz desnu plohu u jedinici vremena iz volumena isteče masa fluida
B = [ru + (dx / 2)
x]
dydz. Istovremeno, kroz desnu plohu u jedinici vremena iz volumena isteče masa fluida
B = [ru + (dx / 2) ![]() (r u) /
(r u) /![]() x]
dydz. Neto dotok mase u jedinici vremena, koji postoji zbog
x-komponente strujanja, jednak je masi koja u volumen uđe u jedinici vremena (A) umanjenoj za masu koja izađe iz volumena u jedinici vremena (B)
x]
dydz. Neto dotok mase u jedinici vremena, koji postoji zbog
x-komponente strujanja, jednak je masi koja u volumen uđe u jedinici vremena (A) umanjenoj za masu koja izađe iz volumena u jedinici vremena (B)
A – B = [ru – (dx / 2)
![]() (r u) /
(r u) /![]() x]
dydz - [ru
+ (dx / 2)
x]
dydz - [ru
+ (dx / 2) ![]() (r u) /
(r u) /![]() x]
dydz = - [
x]
dydz = - [![]() (r u) /
(r u) /![]() x]
dxdydz
= - [
x]
dxdydz
= - [![]() (r u) /
(r u) /![]() x]
dV.
x]
dV.
Analogno možemo odrediti neto dotoke mase u volumen u jedinici vremena, koji postoje zbog komponenti strujanja u
y i z smjeru, - [![]() (rv)/
(rv)/![]() y]
dV i - [
y]
dV i - [![]() (rw)/
(rw)/![]() z]
dV. Odatle je ukupna promjena mase po jedinici vremena, koja postoji zbog trodimenzionalnog strujanja fluida
z]
dV. Odatle je ukupna promjena mase po jedinici vremena, koja postoji zbog trodimenzionalnog strujanja fluida
![]()
Podijelimo li gornji izraz s infinitezimalno malim fiksnim volumenom dV, dobivamo vremensku promjenu mase po jedinici volumena.
![]() (3)
(3)
Budući da je gustoća r = dM/dV
jednaka masi po jedinici volumena, gdje je dM masa elementa volumena, to je vremenska promjena mase po jedinici volumena jednaka vremenskoj promjeni gustoće
![]() r
/
r
/![]() t, što je dalje jednako izrazu (3). Tako dobivamo još jedan oblik jednadžbe kontinuiteta
t, što je dalje jednako izrazu (3). Tako dobivamo još jedan oblik jednadžbe kontinuiteta
![]() (4)
(4)
u kojem je promjena gustoće prikazana preko lokalne promjene ![]() r
/
r
/![]() t.
t.
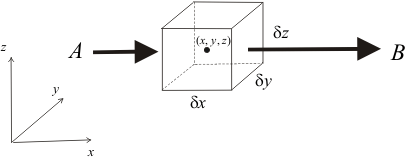
Slika 2. Neto dotok mase u fiksni (Eulerov) element volumena, koji postoji zbog x-komponente strujanja fluida.
Jednadžba stanja idealnog plina (plinska jednadžba, jednadžba stanja)
- zakon do kojeg se dolazi kombinacijom Boyleovog i Charlesovog zakona. Promatramo uzorak zraka konstantne mase m. Neka su početni tlak, temperatura i volumen uzorka p1, T1 i V1. Održavamo najprije temperaturu konstantnom T1 = konst., a tlak povisujemo s vrijednosti p1 na p2. Prema Boyleovom zakonu volumen će se smanjiti na vrijednost V2’ takvu da vrijedi p1V1 = p2V2'. Odatle je V2' = p1V1/p2. Sada održavamo tlak konstantnim p2 = konst., a temperaturu uzorka povisujemo s T1 na T2. Stoga po Charlesovom zakonu volumen mora porasti na vrijednost V2, takvu da vrijedi V2/T2 = V2'/T1. Odatle je V2 = V2'T2/T1 = (p1V1/p2)T2/T1 = p1V1T2/p2T1. Kad pomnožimo jednadžbu V2 = p1V1T2/p2T1 s p2/T2 dobivamo p2V2/T2 = p1V1/T1, što drugim riječima znači da veličina pV/T mora biti konstantna
pV/T = k (1)
gdje je k konstanta proporcionalnosti.
Odredimo konstantu u kombiniranoj plinskoj jednadžbi (1) na temelju vrijednosti pri standardnim uvjetima. Pri standardnim uvjetima volumen jednog kilomola plina mora biti jednak molarnom volumenu Vm = 22.414 m3 kmol-1. Stoga je konstanta k u jednadžbi (1), ako je napišemo za jedan kilomol plina, jednaka univerzalnoj plinskoj konstanti R*:
pVm = R*T . (2)
Promatramo 1 kilomol idealnog plina molekularne mase M. Neka su volumen, temperatura i tlak plina Vm, T i p. Tada je specifični volumen plina a = Vm/M, pa volumen plina možemo izraziti preko specifičnog volumena i molekularne mase: Vm = aM. Uvrstimo u jednadžbu (2) Vm = aM. Dobije se
paM = R*T. (3)
Podijelimo jednadžbu (3) s molekularnom masom. Tako dobivamo jednadžba stanja idealnog plina (4) koja vrijedi za jediničnu masu idealnog plina
pa = (R*/M)T = RT. (4)
Konstanta R = R*/M ovisi o molekularnoj masi idealnog plina i stoga se zove specifična plinska konstanta (J kg-1 K-1).
Pri T = konst. jednadžba stanja (4) svodi se na Boyleov zakon, a uz p = konst. na Charlesov zakon.
Jednadžba stanja idealnog plina može se pisati i drugačije. Prvi ju je izveo Emil Clapeyron 1834. godine i to u obliku
pV = nR*T , (5)
gdje je n je broj kilomolova plina koji se nalazi u masi plina m koja zauzima volumen V. Još jedan oblik plinske jednadžbe je
pV = NkT, (6)
gdje je N broj molekula ili atoma plina koji se nalazi u volumenu plina V, a k je Boltzmannova konstanta. U meteorologiji se plinska jednadžba najčešće koristi u obliku (4).
Primjenom Daltonovog zakona pokazujemo da smjesa idealnih plinova također zadovoljava jednadžbu stanja (4). Promatramo smjesu koja se sastoji od n plinova. Svaki pojedinačni plin, ako je idealan, zadovoljava jednadžbu (4). Za k-ti sastojak, gdje je k = 1,...,n vrijedi
pkak = (R*/Mk)T, (7)
gdje je pk parcijalni tlak, ak je specifični volumen, a Mk je molekularna (atomska) masa k-tog sastojka. Podijelimo jednadžbu (7) sa specifičnim volumenom k-tog sastojka
pk = R*T/(Mkak), (8)
te uvrstimo ak = V/mk, gdje je mk masa k-tog sastojka, a V je volumen smjese. (Uočavamo da sastojak zauzima cijeli volumen smjese). Tako dobivamo jednadžbu
pk = (mk/Mk)R*T/V (9)
na koju primjenjujemo Daltonov zakon:
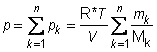 (10)
(10)
Pomnožimo jednadžbu (10) sa specifičnim volumenom smjese a = V/m, gdje je m ukupna masa smjese m = amk. Tako dobivamo
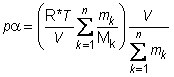 (11)
(11)
Uvedemo u jednadžbu (11) prividnu molekularnu masu smjese M, gdje
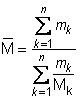 (12)
(12)
Tako dobivamo
![]() (13)
(13)
čime smo pokazali da smjesa idealnih plinova, čija je prividna molekularna masa jednaka harmoničkom srednjaku molekularnih masa sastojaka Mk ponderiranih masom sastojka mk, zadovoljava jednadžbu stanja idealnog plina.
Vidi idealni plin, jednadžba stanja realnog plina, Boyleov zakon, Charlesov zakon, Daltonov zakon.
Jednadžba gibanja u sfernim koordinatama
- vidi pdf dokument.
Jednadžba gibanja u sustavu koji rotira
- vidi pdf dokument.
Jednadžba stanja realnog plina
- Kako realni plin ima veću gustoću od idealnog plina, njegovo ponašanje odstupa od ponašanja idealnog plina. Zbog veće gustoće, prosječna udaljenost susjednih molekula ili atoma (r) u realnom plinu dovoljno je mala da potencijalna energija (Ep) bitno utječe na ponašanje plina (slika 1). Radijus udaljenosti čestica za koji je Ep = 0, naziva se van der Waalsov radijus. Ako je udaljenost među česticama manja od van der Waalsovog radijusa (plin je dovoljno gust), potencijalna energija je pozitivna, pa se čestice međusobno odbijaju. Ako je udaljenost među česticama veća od van der Waalsovog radijusa, čestice se međusobno privlače. Međutim, slika 1 pokazuje da su privlačne sile među česticama rjeđih plinova puno slabije od odbojnih sila među česticama gušćih plinova. Nadalje, kako r raste, tako i Ep teži k nuli. To drugim riječima znači da je utjecaj potencijalne energije na ponašanje plina male gustoće zanemariv.
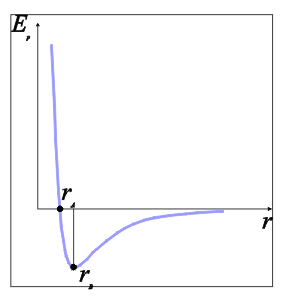
Slika 1. Potencijalna energija dviju molekula ili atoma (Ep) kao funkcija međusobne udaljenosti promatranih čestica (r). Radijus udaljenosti čestica r = rA, za koji je Ep = 0, naziva se van der Waalsov radijus. Za radijus udaljenosti r = rB potencijalna energija čestica je minimalna. U području Ep > 0, čestice se međusobno odbijaju, a u području Ep < 0, čestice se privlače.
Očito je da stanje realnog plina moramo opisati jednadžbom koja je kompliciranija od jednadže stanja idealnog plina. Takva jednadžba mora obuhvaćati i privlačenje i odbijanje molekula ili atoma plina. Postoji više jednadžbi stanja realnog plina, od kojih se najčešće upotrebljava van der Waalsova. (Inače, njezin autor, nizozemski znanstvenik Johannes Diderik van der Waals (1837-1923) je zbog svog doprinosa vezanog uz jednadžbu stanja plinova i tekućina 1910. godine dobio Nobelovu nagradu iz fizike.).
Pretpostavimo da se čestice plina (molekule ili atomi) ponašaju poput tvrdih kuglica. Međusobno odbijanje čestica možemo tada objasniti činjenicom da dvije čestice ne mogu istovremeno zauzimati isti volumen. Označimo volumen plina s V, a volumen koji zauzimaju čestice plina sa nb, gdje je V >> nb, n je broj kilomolova plina, a b je konstanta koja ovisi o termodinamičkom gibanju čestica. Tada je efektivni volumen plina (volumen unutar kojeg se čestice mogu gibati), Vef = V-nb. Uvođenjem efektivnog volumena uvažili smo efekte odbijanja čestica pojednostavljenim pristupom klasične fizike (dublje objašnjenje odbijanja čestica na malim udaljenostima dala je tek kvantna fizika).
Privlačenje čestica uvažit ćemo uvođenjem efektivnog broja molekula ili atoma Nef. Privlačenje čestica dovodi do njihovog udruživanja, čime efektivni broj čestica postaje manji. Što je gustoća plina veća, to je prividno smanjenje broja čestica efikasnije. Nadalje, privlačenje čestica je to slabije što je temperatura plina veća, budući da s porastom temperature rastu i brzine gibanja čestica, odnosno njihova kinetička energija. Što je brzina čestica veća, to je veća i mogućnost da se čestice međusobno više udalje. Stoga s porastom temerature opada potencijalna energija (slika 1) i u skladu s tim, slaba privlačna sila među česticama sve više slabi. Prema tome, za efektivni broj čestica vrijedi Nef = N(1–Cn/TV), gdje je N stvarni broj molekula ili atoma plina, T je temperatura plina, a C je konstanta. Pri tom ćemo pretpostaviti da je Cn/TV << 1.
Jednadžbu stanja realnog plina možemo formalno napisati polazeći od jednadžbe stanja idealnog plina, ali ćemo sada umjesto stvarnog volumena plina imati efektivni volumen, a umjesto stvarnog broja molekula ili atoma efektivni broj. Tako dobivamo
pVef = NefkT. (1)
Uvrštavanjem Vef = V - nb i Nef = Nef = N (1 – C n / TV) dobivamo
p(V - nb) = N (1 – C n / TV)kT, (2)
gdje je k Boltzmannova konstanta. Odatle je Nk = NR*/NA = nR*, gdje je n broj kmolova plina, pa jednadžbu (2) nakon množenja s (1+C n / TV) možemo pisati
p( V - nb)(1+ C n / TV) = nR*[1–(Cn/TV)2]T . (3)
Budući je C n / TV << 1, član (C n / TV)2 možemo zanemariti, pa jednadžba stanja realnog plina prelazi u
(p+Cpn/TV)(V - nb) = nR*T . (4)
Umjesto omjera p/T u članu C p n / TV uvrstiti ćemo približnu vrijednost dobivenu na temelju jednadžbe stanja idealnog plina. Uvrštavanjem p/T = nR*/V u (4) i supstitucijom a = CR*, gdje je a konstanta, dobivamo van der Waalsovu jednadžbu
(p+an2/V2)(V-nb) = nR*T , (5)
gdje su vrijednosti van der Waalsovih konstanti a i b za neke tvari prikazane u tablici 1.
Tablica 1. Van der Waalsove konstante a i b, kritični tlak (pc) i kritična temperatura (Tc) za neke plinove.
| Tvar | a (J m3 mol-2) | b (m3 mol-1) | pc (Pa) | Tc (K) |
| zrak | 0.1358 | 3.64 . 10-5 | 3.77 . 106 | 133 |
| N2, dušik | 0.1361 | 3.85 . 10-5 | 3.39 . 106 | 126.2 |
| He, helij | 0.00341 | 2.34 . 10-5 | 0.23 . 106 | 5.2 |
| CO2, ugljikov dioksid | 0.3643 | 4.27 . 10-5 | 7.39 . 106 | 304.2 |
| H2, vodik | 0.0247 | 2.65 . 10-5 | 1.30 . 106 | 33.2 |
| H2O, vodena para | 0.5507 | 3.04 . 10-5 | 22.09 . 106 | 647.3 |
| NH3, amonijak | 0.4233 | 3.73 . 10-5 | 11.28 . 106 | 406 |
| CCl2F2, freon | 1.078 | 9.98 . 10-5 | 4.12 . 106 | 385 |
Za razliku od jednadžbe stanja idealnog plina, van der Waalsova jednadžba (5) je jednadžba trećeg stupnja u volumenu. To znači da jednoj vrijednosti tlaka pripadaju tri različite vrijednosti volumena. Ako izoterme određene na temelju van der Waalsove jednadžbe prikažemo u (V,p) dijagramu, dobiti ćemo sliku poput slike 2, izuzev dijelova izotermi koje se nalaze unutar osjenčanog područja. U osjenčanom području izoterme određene iz van der Waalsove jednadžbe imaju oblik poput izoterme T prikazane zelenom krivuljom. Na dijelu te krivulje, počev od točke A pa do točke B, pri porastu volumena povećava se i tlak. Takvo ponašanje nije stvarno fizikalno ponašanje plina, već je odraz aproksimativnosti Waalsove jednadžbe. Stvarne izoterme unutar osjenčanog područja paralelne su s x osi, te se unutar tog područja tlak ne mijenja porastom volumena. Izoterma Tc je takva da u točki (Vc, pc) ima infleksiju. Ta točka naziva se kritična točka, a Tc, Vc i pc su kritične vrijednosti temperature, tlaka i volumena (vidi tablicu 1). Za temperature više od kritične van der Waalsova jednadžba dobro opisuje ponašanje realnog plina.
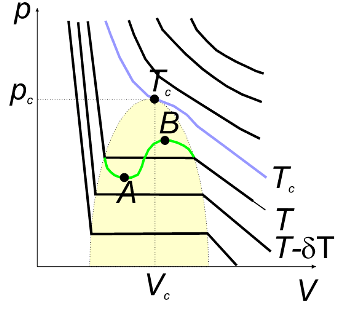
Slika 1. Izoterme određene iz van der Waalsove jednadžbe prikazane u (V,p) dijagramu, gdje je V volumen, a p tlak. Budući da je van der Waalsova jednadžba jednadžba trećeg stupnja u volumenu, izoterme su krivulje trećeg stupnja (jednoj vrijednosti tlaka pripadaju tri vrijednosti volumena), pa unutar osjenčanog područja imaju oblik poput onog prikazanog za temperaturu T zelenom krivuljom. To znači da duž intervala AB tlak raste pri porastu volumena. Takvo ponašanje izotermi odraz je aproksimativnosti van der Waalsove jednadžbe, te ne odgovara fizikalnoj realnosti. Stvarne izoterme unutar osjenčanog područja imaju takav oblik da pri porastu volumena tlak ostaje konstantan, kao što je prikazano punim linijama unutar osjenčanog područja. Kritična točka (Vc,pc) na izotemi Tc je točka infleksije.
Van der Waalsovu jednadžbu (5) možemo dalje preurediti tako da na lijevoj strani prikažemo tlak plina
p = nR*T/(V-nb)-an2/V2. (6)
Iz gornje jednadžbe vidimo da je tlak plina p umanjen za veličinu an2 /V2 zbog privlačenja molekula ili atoma plina. Član an2 /V2 naziva se
tlakom kohezije. Nadalje, iz iste jednadžbe možemo odrediti i kritični volumen, temperaturu i tlak
(Tc, Vc i pc). Za točku infleksije mora vrijediti
(![]() p/
p/![]() V)T=Tc
= 0 i (
V)T=Tc
= 0 i (![]() 2p/
2p/![]() V2)T=Tc
= 0. Odatle je
V2)T=Tc
= 0. Odatle je
(![]() p/
p/![]() V)T = -nR*Tc/(Vc-nb)2+2an2/Vc3 = 0,
(7)
V)T = -nR*Tc/(Vc-nb)2+2an2/Vc3 = 0,
(7)
(![]() 2 p /
2 p /![]() V2)T = 2nR*Tc/(Vc-nb)3–6an2/Vc4 = 0.
(8)
V2)T = 2nR*Tc/(Vc-nb)3–6an2/Vc4 = 0.
(8)
Pomnožimo jednadžbu (7) s 2/(Vc-nb) i zatim je pribrojimo jednadžbi (8). Dobivamo
4an2/[Vc3(Vc-nb)]-6an2/Vc4 = 0, (9)
iz čega slijedi Vc = 3nb. Uvrstimo Vc = 3 nb u jednadžbu (7) i zatim odredimo kritičnu temperaturu Tc = 8a/(27bR*). Kritični tlak možemo odrediti uvrštavanjem Vc i Tc u van der Waalsovu jednadžbu (6). Tako dobivamo pc = a/(27b2).
Pomnožimo van der Waalsovu jednadžbu (6) s volumenom V i preuredimo
pV = nR*TV/(V-nb)-an2/V = nR*T[(1-nb/V)-1–(n/V)(a/R*T)]. (10)
Budući je V >> nb, ispunjen je uvjet |nb/V| < 1, pa član (1-nb/V)-1 možemo razviti u red (za
|x| < 1 funkciju (1–x)-1 možemo razviti u red (1 –x)-1
= 1+x+x2+x3+x4+...) i zanemariti više potencije od
nb/V. Tako dobivamo (1-nb/V)-1 ![]() 1+nb/V. Nakon uvrštavanja u jednadžbu (10) i sređivanja dobivamo
1+nb/V. Nakon uvrštavanja u jednadžbu (10) i sređivanja dobivamo
pV = nR*T[1+(n/V)(b-a/R*T)]. (11)
Što je omjer broja kilomolova plina i volumena plina n/V manji, gustoća plina je manja, a jednadžba (11) je to sličnija jednadžbi stanja idealnog plina.
Kako su kritične temperature atmosferskih sastojaka izuzev vodene pare i uljikovog dioksida daleko niže od atmosferskih temperatura (vidi tablicu 1), ponašanje atmosfere sasvim dobro je opisuje i jednadžba stanja idealnog plina, koja je od jednadžbe realnog plina jednostavnija. Stoga se u meteorologiji umjesto jednadžbe stanja realnog plina koristi jednadžba stanja idealnog plina.