POJMOVNIK - T
Temperatura
- fizikalna veličina mjerljiva termometrom. Temperatura nekog tijela povezana je sa srednjim slučajnim gibanjem molekula u tijelu. Tijela koja se nalaze u toplinskoj ravnoteži imaju jednaku temperaturu. Kod plinova temperatura ovisi o kinetičkoj energiji molekula. Za idealni plin temperatura je omjer unutarnje energije i specifične topline pri konstantnom volumenu. Zrak se ponaša poput idealnog plina. U meteorologiji temperaturu u teorijskim razmatranjima izražavamo u stupnjevima Kelvina (K), a u praktičnoj primjeni u stupnjevima Celzijusa gdje vrijedi 0ºC= 273.15 K. U anglosaksonskim zemljama u upotrebi su i stupnjevi Fahrenheita, gdje °F = (9/5)°C + 32.Temperatura mokrog termometra
(1) Izobarna temperatura mokrog termometra (Tw,i) je temperatura koju bi imala čest ako bi se pri konstantnom tlaku adijabatski ohladila do zasićenja isparavanjem vode ili sublimacijom leda u čest. Pri tom se čest ohlađuje jer troši toplinu na isparavanje/sublimaciju. Ovu temperaturu očitavamo s mokrog termometra na psihrometru. Također, kapljice unutar oblaka, ako isparavaju, ohlađuju se pri tom do temperature Tw,i. Nadalje, Tw,i se razlikuje od rosišta Td i općenito je Tw,iŠto je zrak vlažniji, to je razlika između temperature zraka (T) i izobarne temperature mokrog termometra (Tw,i) manja. Tu razliku T-Tw,i nazivamo psihrometrijska razlika i upotrebljavamo je kod određivanja tlaka vodene pare e
![]()
gdje je e tlak vodene pare, es je maksimalni (ravnotežni) tlak vodene pare nad vodenom ili ledenom površinom pri temperaturi T, p je tlak zraka, L je latentna toplina (L = Llv u slučaju isparavanja, a u sublimacije L = Liv), e je omjer specifičnih plinskih konstanti suhog zraka i vodene pare, a je srednjak specifične topline vlažnog zraka pri konstantnom tlaku.
(2) Adijabatska temperatura mokrog termometra (Tw,a) je temperatura koju bi imala čest zraka ako bi se suhoadijabatskom ekspanzijom ohladila do zasićenja te zatim mokroadijabatski komprimirala do početnog tlaka p. Može se odrediti grafički pomoću termodinamičkog dijagrama (vidi sliku 1). Kako se čest pri adijabatskoj kompresiji grije, to je adijabatska temperatura mokrog termometra veća od izobarne Tw,a>Tw,i.

Slika 1. Grafičko određivanje adijabatske temperature mokrog termometra Tw,a pomoću kosog emagrama. Nezasićena čest se u početku nalazi na tlaku p i temperaturi T (točka A). Čest se zatim suhoadijabatski hladi sve dok ne postane zasićena - pratimo suhu adijabatu od početne točke A pa do kondenzacijske razine (točka B) koja se nalazi na temperaturi Tk i tlaku pk. Dalje se čest mokroadijabatski komprimira sve do početnog tlaka – pratimo mokru adijabatu od točke B do točke C u kojoj je tlak jednak početnom tlaku p, a temperatura je jednaka adijabatskoj temperaturi mokrog termometra Tw,a.
Temperaturna inverzija
- porast temperature s visinom. Javlja se npr. pri noćnom ohlađivanju, ili pri prodoru hladnog zraka tako da se sloj hladnijeg (gušćeg) zraka nađe ispod sloja toplog (rjeđeg) zraka. Tada je atmosfera statički stabilna.Vidi vertikalni temperaturni gradijent.
Termalni vjetar
- vidi pdf dokument.Termodinamičke varijable (varijable stanja)
- varijable koje potpuno opisuju stanje promatranog termodinamičkog sustava. Varijable stanja česti fluida mase m jesu tlak (p), temperatura (T) i volumen (V). Tlak je skalarna veličina definirana kao sila po jedinici površine. Zbog magnitude tlaka u atmosferi uobičajena jedinica tlaka u meteorologiji je hPa (hektopaskal), gdje je 1 hPa = 100 Pa = 100 N m-2 = 100 kg m-1 s-2 = 1 mb. Prosječni tlak na razini mora iznosi 1013.2 hPa, pa se tlak katkad izražava i u jedinicama normalne atmosfere (N atm.), gdje 1 N atm. = 1013.2 hPa. U tehničkoj literaturi koristi se i jedinica tehnička atmosfera (T atm.), gdje je 1 T atm. = 1 kp cm-2.Temperatura je manifestni oblik topline, a u jednadžbama dinamičke meteorologije izražava se u Kelvinima (K): T = t + 273.15, gdje je T temperatura (K), a t temperatura (oC). Volumen se u meteorologiji izražava u kubičnim metrima.
Čest mase m i volumena V ima gustoću r, koja ovisi samo o masi i volumenu česti: r=m/V. Stoga umjesto volumena kao varijablu stanja možemo koristiti gustoću r (kg m-3) ili njenu recipročnu vrijednost a = r-1 = V/m, gdje je a (m3 kg-1) specifični volumen. Pri tlaku od 1 N atm. i temperaturi od 0oC gustoća i specifični volumen zraka imaju ove vrijednosti: r = 1.293 kg m-3 i a = 0.773 m3 kg-1.
Djelovanjem nekog procesa (npr. dodavanjem topline ili komprimiranjem česti vanjskom silom) stanje česti će se promijeniti – sustav će doći u novo termodinamičko stanje u kojem varijable stanja imaju nove vrijednosti. Te nove vrijednosti potpuno opisuju novo stanje česti. Tako npr., ako česti dodajemo toplinu, tako da joj volumen ostane konstantan, temperatura česti će porasti.
Uz tlak, temperaturu, volumen i gustoću postoje i druge varijable stanja, poput entropije, unutarnje energije i drugih. Termodinamičke varijable dijelimo na ekstenzivne i intenzivne. Ekstenzivne su one čija vrijednost poraste toliko puta koliko puta povećamo količinu materije. Na primjer, ako udvostručimo masu promatranog plina (zadržavši sve ostale uvjete nepromijenjenima), udvostručit će se njegov volumen, unutarnja energija i vrijednosti drugih ekstenzivnih varijabli. Za razliku od toga, vrijednosti intenzivnih varijabli ne ovise o količini materije (npr. temperatura).
Termodinamički dijagram (adijabatski dijagram)
- dijagram koji prikazuje vrijednosti tlaka, temperature, omjera miješanja, gustoće, ili njihovih funkcija poput jednadžbe stanja, Clausius-Clapeyronove jednadžbe, prvog stavka termodinamike za adijabatske procese. Termodinamičkih dijagrama ima više (npr. emagram, tefigram, Stüvegram itd.). Međusobno se razlikuju se po izboru koordinatnih osi, ali se svaki može dobiti matematičkim transformacijama iz drugih termodinamičkih dijagrama. Svi ti dijagrami uvijek sadrže izobare, izoterme, izolinije maksimalnog omjera miješanja te suhe i mokre adijabate. Reverzibilan proces u termodinamičkom dijagramu prikazan je zatvorenom krivuljom. Ako je površina koju takva krivulja zatvara na bilo kojem dijelu dijagrama proporcionalna radu koji termodinamički sustav učini pri procesu, onda se takav dijagram zove pravi termodinamički dijagram.Jedan od pravih termodinamičkih dijagrama koji se često koristi u praksi je kosi emagram (vidi sliku) na čijoj je apscisi temperatura, a na ordinati negativni logaritam tlaka. Koordinatne osi zatvaraju kut od približno 135 stupnjeva kako bi kut između izotermi i suhih adijabata bio što veći.

Kosi emagram (T, - ln p) sadrži izobare, izoterme, suhe i mokre adijabate te izolinije maksimalnog omjera miješanja.
Termodinamički sustav
- materijalna čest čije promjene stanja promatramo. Do promjena stanja, odnosno promjena vrijednosti termodinamičkih varijabli dolazi uslijed različitih fizikalnih procesa.Termodinamika
- dio fizike koji se odnosi na procese koji uključuju transformaciju topline u mehanički rad, mehaničkog rada u toplinu ili tok topline s toplijeg na hladnije tijelo. Termodinamika uvodi pojam temperature, koji ne postoji u klasičnoj mehanici. Klasična termodinamika proučava ravnotežna stanja, koncentrirajući se na početne i konačne uvjete, a ne bavi se međuprocesima koji se događaju tijekom prelaska iz početnog u konačno stanje. U meteorologiji, termodinamika se odnosi na promjene stanja česti do kojih dolazi uslijed različitih fizikalnih procesa.Prvi stavak termodinamike kaže da je unutarnja energija (link unutarnja energija) izoliranog termodinamičkog sustava (onog za koji nema nikakvog međudjelovanja s okolišem) konstantna. Ako sustav nije izoliran, unutarnja energija mu se može promijeniti zbog dva makroskopska procesa: rada učinjenog na sustavu i toplini razmijenjenoj s okolišem:
du = đq + dw,
gdje je du promjena unutarnje energije po jedinici mase, đq promjena topline po jedinici mase (đ je geometrijski a ne totalni diferencijal), a dw je rad učinjen sustavu po jedinici mase. Za jednostavni termodinamički sustav, u kojem je rad samo posljedica promjene volumena, vrijedi dw = - p da, gdje je p tlak, a a je specifični volumen. Tada prvi stavak termodinamike možemo pisati ovako:
đq = du + p da.
Unutarnja energija idealnog plina ovisi samo o temperaturi plina T, du = cv dT, gdje je cv specifična toplina pri konstantnom volumenu. Stoga u atmosferi, koja se ponaša poput idealnog plina, vrijedi ovaj oblik prvog stavka termodinamike:
đq = cv dT + p da.
Gornji izraz možemo preurediti upotrebom jednadžbe stanja idealnog plina u obliku p a = R T, gdje je R specifična plinska konstanta te primjenom Mayerove relacije. Tako dolazimo do prvog stavka termodinamike u obliku koji se najčešće koristi u meteorologiji.
đq = cp dT - a dp.
Drugi stavak termodinamike kaže da svaki fizikalni sustav posjeduje entropiju. Za svemir u cjelini te za svaki izolirani sustav (onaj za kojeg nema nikakvog međudjelovanja s okolišem) vremenska promjena specifične entropije mora biti
ds/dt >= 0,
gdje je za reverzibilne (ravnotežne) procese ds/dt = 0, a za ireverzibilne (spontane) procese ds/dt > 0. Drugim riječima, entropija sustava nikada se ne može smanjivati. Kako gornji izraz uključuje i reverzibilne i ireverzibilne procese, ovaj oblik drugog stavka termodinamike nazivamo generaliziranim.
Entropija se može mijenjati zbog dolaska sustava u kontakt s okolišem (des) ili zbog promjena unutar samog sustava (dis):
ds = des + dis ,
gdje je des = đq / T, a đq je toplina dodana sustavu po jedinici mase. Za reverzibilne procese nema promjene specifične entropije unutar samog sustava dis = 0, dok za ireverzibilne procese, koji se događaju spontano, mora biti dis > 0. Stoga generalizirani drugi stavak termodinamke možemo prikazati i ovako:
ds >= đq / T.
Primjenimo li na gornju jednadžbu prvi stavak u obliku đq = du + p da, dobivamo još jedan oblik generaliziranog drugog stavka termodinamike:
T ds >= du + p da.
U meteorologiji najčešće proučavamo ravnotežna stanja te stoga koristimo drugi stavak u obliku
ds = des = đq / T,
odnosno
T ds = du + p da = cv dT + p da = cp dT - a d p.
Treći stavak termodinamike (Nernstov teorem) kaže da entropija svih termodinamičkih sustava na apsolutnoj nuli (T = 0 K = -273.15oC) ima dobro definiranu donju granicu. Kako su atmosferske temperature daleko iznad apsolutne nule, u meteorologiji se ovaj stavak ne primjenjuje.
Vidi termodinamički sustav, termodinamičke varijable, entropija.
Termosfera
- vidi strukturu atmosfere.Tlak
- napetost koja je jednolika u svim smjerovima. Na promatranoj plohi mjerimo ga kao neto silu u smjeru normale na izloženu plohu podijeljenu s površinom plohe. Dinamički, tlak je dio tenzora napetosti koji ne ovisi o viskoznosti već ovisi samo o molekularnom gibanju pri danoj temperaturi i gustoći.Tlak zraka ili atmosferski tlak označavamo slovom p te ga u meteorologiji izražavamo u hektopaskalima (1 hPa = 100 N m-2). Kako je zrak smjesa suhog zraka i vodene pare, te kako za smjesu plinova vrijedi Daltonov zakon, to ukupni atmosferski tlak možemo prikazati kao zbroj tlaka suhog zraka pd i tlaka vodene pare e:
p = pd + e.
Ako je zrak zasićen vodenom parom, tada je tlak vodene pare jednak maksimalnom (ravnotežnom) tlaku vodene pare es.
U atmosferi pomoću barometra mjerimo ukupni atmosferski tlak p, a tlak vodene pare e možemo izračunati na temelju mjerenja psihrometrom (vidi izobarnu temperaturu mokrog termometra). Ravnotežni tlak vodene pare es uz poznatu temperaturu T računamo iz integralnog oblika Clausius-Clapeyronove jednadžbe.
Na srednjoj razini mora vrijednosti atmosferskog tlaka kreću se u rasponu od oko 960 do 1050 hPa. Područje sniženog tlaka sinoptičkih razmjera nazivamo ciklonom, a područje povišenih vrijednosti anticiklonom.
Za procese većih (sinoptičkih) razmjera (vidi analizu skala) približno vrijedi hidrostatička ravnoteža. Odatle primjenom hidrostatičke jednadžbe dolazimo do izraza koji prikazuje eksponencijalno opadanje atmosferskog tlaka s visinom (vidi sliku 1):
![]()
gdje je p(z) tlak na nadmorskoj visini z, pNN je tlak na srednjoj razini mora, g je akceleracija sile teže, R je specifična plinska konstanta za zrak, a T je gdje je srednja temperatura sloja zraka od srednje razine mora do visine z:
![]()
gdje su T(z) i TNN temperature na visini z i na srednjoj razini mora.
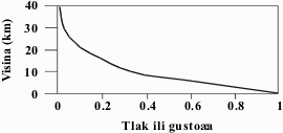
Slika 1. Shematski prikaz prosječne promjene tlaka s visinom u atmosferi. Tlak se s visinom postepeno smanjuje te se asimptotski približava k nuli. Na isti način ponaša se i gustoća zraka.
Toplinsko (dugovalno, infracrveno, IC) zračenje
- zračenje valnih duljina u rasponu od 0.7 do 400 mm.Vidi sastav atmosfere, radijacijsko-apsorpcijska svojstva sustava Zemlja-atmosfera.
Tornado
- Naziv tornado potječe od španjolske riječi tornada (što znači grmljavinska oluja). Tornado je vertikalni stupac zraka koji brzo rotira, a proteže se od oblaka kumulonimbusa (link kumulonimbus) (Cb) do tla. Češće se događa nad vodenom podlogom nego nad tlom, i tada ga nazivamo morska pijavica (link pijavica). Katkad, brzina vjetra pri tlu u tornadu može dostići i do 135 m s-1 (oko 490 km h-1), iako su najčešće brzine manje. Na sjevernoj hemisferi rotacija u tornadu najčešće je ciklonalna, a tek vrlo rijetko anticiklonalna. Većina tornada ima samo jedan vertikalni stupac rotirajućeg zraka, ali neki imaju dva ili više manjih vrtloga koji rotiraju oko zajedničkog središta osnovnog tornada.Tornado je lako uočljiv po tome što pri tlu u njemu rotiraju ostaci pojedinih predmeta podignutih s tla, dok se u visini vidi ljevkasto područje u kojem dolazi do kondenzacije. Pri tom se često najprije uočava rotirajući stupac predmeta podignutih s tla, a kondenzacijski lijevak se formira nešto kasnije. Katkad se ljevkasti oblak ne vidi, ili je tornado zakriven oborinom Tijekom zamiranja tornada kondenzacijski lijevak postaje uzak, deformira se i produžuje poput užeta, te naginje toliko da postaje gotovo horizontalan.
Najveći i najrazorniji tornadi nastaju u dugotrajnim (duljim od 1 h) rotirajućim olujama koje se nazivaju superćelije. Takvi tornadi često više puta prolaze kroz životni ciklus od 20 do 30 minuta, ponovno se pojavljujući duž putanje oluje 'roditelja'. Tornadi se u superćelijama obično formiraju ispod ciklonalno rotirajućeg oblačnog zida, tj. snižene baze oblaka u kojoj nema oborine. Tu se u osnovnu uzlaznu struju oluje usisava relativno vlažan, i zbog isparavanja, ohlađen zrak. Oblačni zid se često nalazi na stražnjoj strani oluje koja se giba. Primijećeno je da se tornadi koji rotiraju anticiklonalno nalaze duž udarne fronte oluje.
Tornadi se mogu pojaviti i u običnim olujama koje nisu superćelijske. U tom slučaju se razvijaju tijekom razvojne faze konvekcijske ćelije. Takvi tornadi vezani su uz relativno slabe oluje i ne traju dulje od 30 do 40 minuta.
U rijetkim slučajevima tornadi se javljaju i u frontalnim područjima oborine. Kratkotrajni tornadi i ljevkasti oblaci viđeni su također i u olujama koje nisu superćelijske te se nalaze u blizini relativno hladnih visinskih dolina niskog tlaka.
Karakteristična prostorno-vremenska skala (vidi analizu skala) za tornado:
| U ~ 100 m s-1 | skala horizontalne brzine |
| W ~ 10 m s-1 | skala vertikalne brzine |
| L ~ 100 m | skala duljine |
| H ~ 104 m | skala visine |
| dP/L ~ 40 Pa m-1 | skala horizontalnih fluktuacija tlaka |
Kako je tornado kratkotrajan proces malih razmjera i istovremeno veoma velikih brzina vjetra, mjerenja meteoroloških veličina u njemu su složena, skupa i oskudna. Tijekom posljednjih desetljeća prikupljeno je tek ponešto izmjerenih podataka koji su većinom dobiveni Doppler radarom visoke rezolucije i ekstenzivnim vizulalnim opažanjima. O temperaturi unutar tornada malo se zna, kao i o maksimalnim mogućim brzinama vjetra. Također, za sad se još ne zna se ni točan izvor rotacije u tornadu. Međutim, poznato je da vertilkalne brzine u tornadu mogu ići i do 80 m s-1.
Pri proučavanju tornada uz mjerene podatke koristimo i laboratorijske eksperimente te numeričke modele vrtloga nalik na tornado. Na taj način moguće je reproducirati neka od svojstava koja se uočavaju i u realnom tornadu. Tako je ustanovljeno da vrtlog tornada rotira poput krutog tijela - unutar tornada obodna brzina proporcionalna je udaljenosti od središta tornada dok izvan tornada vrlo brzo opada. Pri tlu zrak brzo konvergira u tornado. Katkad se zrak u središtu tornada može spuštati, a u području daljem od središta uzdizati. Idući od ruba prema središtu tornada, tlak jako opada. Međutim, štete koje uzrokuje tornado, ne nastaju zbog nagle promjene tlaka, već zbog velike napetosti vjetra, koja je proporcionalna kvadratu brzine. Budući da su dimenzije tornada male, a brzine vjetra u tornadu vrlo velike, centrifugalna sila (koja je usmjerena radijalno prema van od središta tornada) veća je od sile gradijenta tlaka (koja je usmjerena radijalno prema središtu tornada). Zbog toga predmeti koje tornado podigne u zrak često bivaju izbačeni izvan samog tornada. Približno se obodna brzina u tornadu može aproksimirati ciklostrofičkim vjetrom.
Mehanizam nastanka tornada još uvijek nije potpuno objašnjen. Katkad se sinoptički uvjeti mogu činiti veoma povoljnima za nastanak tornada, no on se ipak ne pojavi, što drugim riječima znači da su za nastanak tornada bitni lokalni uvjeti. Čini se da su za tornado relevantni slijedeći parametri (tablice I - III): bulk-Richardsonov broj RiB, konvekcijska raspoloživa potencijalna energija CAPE, spiralnost u odnosu na oluju SRH, EHI indeks, energija inhibicije konvekcije CIN, razina slobodne konvekcije LFC, razina bez uzgona LNB, indeks dizanja LI, parametar generiranja vrtložnosti VGP te relativna brzina vjetra u odnosu na oluju V-c, gdje je c vektor gibanja oluje, a V je vektor vjetra u okolišu. Međutim, tablice I - III ukazuju na širok raspon vrijednosti promatranih parametara potvrđujući tako da su naša saznanja o tornadu još uvijek nedovoljna.
Tablica I. Vrijednosti nekih parametara za tornado.
| referenca | RiB | CAPE (J kg-1) | SRH (J kg-1) sloj 0-3 km | EHI | CIN (J kg-1) | LFC (m) | LNB (m) | LI (K) |
| de Coning i sur. (2002) | 7-16 | 564 - 1914 | -423 do -354 | -3.8 do 1 | -6.2 do -2.2 | |||
| Garner i Thalken (2002) | 966 - 6142 | 44-316 | 0.9 - 8.4 | 1055 - 3679 | ||||
| Hannesen i sur. (1998) | 25 | 70 - 440 | -4 do 105 | -0.002 do 0.3 | 1200 | 7200 | ||
| Rogash i Racy (2002) | 3200 | 280 | ||||||
| Thompson i Edwards (2000) | 2200 - 5000 | 80 - 400 | <10 - 100 | 2000 |
Tablica II. Vrijednosti parametara pogodne za pojavu tornada (Garner i Thalken, 2002).
| parametar | EHI | LFC (m) | VGP | |V-c| (m s-1) |
| pogodno za nastanak tornada | 1.0 | 2500 | 0.3 | 10 |
| vrlo pogodno za nastanak tornada | 2.0 | 1800 | 0.6 | 20 |
| izuzetno povoljno za nastanak tornada | 4.0 | 1200 | 1.0 | 25 |
Tablica III. Procjena opasnosti od tornada induciranog superćelijom na temelju EHI indeksa (Davies, 1993).
| EHI | |
| < 2.0 | nije vjerojatan tornado induciran mezociklonom |
| 2.0 - 2.4 | tornado induciran mezociklonom je vjerojatan, ali nije vjerojatno da bude jak ili dugotrajan |
| 2.5 - 2.9 | jerojatnost pojave tornada induciranog mezociklonom |
| 3.0 - 3.4 | moguć jak tornado (F3) |
| > 3.4 | moguć razoran tornado |
- Davies, J. M., 1993: Hourly helicity, instability, and EHI forecasting supercell tornadoes. Preprints – 17th Conference on Severe Local Storms. St. Louis, Missouri, Amer. Meteorol. Soc-. 588-592.
- de Coning, E., Adam, B. F., Goliger, A. M., van Wyk, T., 2002: An F3 tornado in Heidleberg, South Africa on 21 October 1999. National Weather Association Electronic Journal of Operational Meteorology. http://www.nwas.org/ej/heidelberg/.
- Garner, J. M., Thalken, B. W., 2002: Evaluation of an experimetnal tornado index. http://www.garnerchase.net/tornado_index.html.
- Hannesen, R., Dotzek, N., Gysi, H., Beheng, K. D., 1998: Case study of a tornado in the Upper Rhine valley. Meteorol. Z., N. F. 7, 163-170.
- Rogash, J. A., Racy, J., 2002: Some meteorological characteristics of significant tornado events occurring in proximity to flash flooding. Wea. Forecasting, 17, 155-159.
- Thompson, R. L., Edwards, R., 2000: An overwiev of environmental conditions and forecast implications of the 3 May 1999 tornado outbreak. . Wea. Forecasting, 15, 682-699.
TORRO ljestvica
- ljestvica za ocjenu jakosti tornada i pijavice. Prikladna je za tip izgradnje i naseljenosti u Europi. Detaljnija je od Fujita ljestvice.
| jakost | naziv tornada |
brzina vjetra |
opis učinaka i šteta | |
| m s-1 | km h-1 | |||
| T0 | slabi | 17 - 24 | 61 - 86 | Razbacani sitni predmeti i smeće spiralno se podižu s tla, grane se lome; na poljima se može vidjeti putanja tornada. |
| T1 | blagi | 25 - 32 | 87 - 115 | Vrtni namještaj i lagani predmeti se prevrću i mogu biti nošeni zrakom. Drvene ograde se prevrću. Na stablima lomovi; manja oštećenja na crijepovima, olucima i lakim građevinama. |
| T2 | umjereni | 33 - 41 | 116 - 148 | Automobili i prikolice mogu se pomaknuti; krovovi garaža odneseni vjetrom; mnogo šteta na stablima, krovovima i dimnjacima; manja stabla iščupana. |
| T3 | jaki | 42 - 51 | 149 - 184 | Brojni automobili i prikolice prevrnuti; garaže uništene; na krovovima kuća vidljive grede; automobili u vožnji pogurnuti s ceste; nekoliko većih stabala oboreno ili ičupano s ceste. |
| T4 | žestoki | 52 - 61 | 185 - 220 | Velike štete na vozilima i prikolicama; neke šupe i štaglji nošeni zrakom na znatne udaljenosti; čitavi krovovi kuća odneseni; brojna stabla prevrnuta ili iščupana. |
| T5 | snažni | 62 - 72 | 221 - 259 | Automobili podignuti uvis; ozbiljnije štete na zgradama, no zidovi ostaju neoštećeni; najslabije stare zgrade se urušavaju. |
| T6 | umjereno razorni | 73 - 83 | 260 - 299 | Teška vozila podignuta u zrak; čvrste kuće ostaju bez cijelih krovova, a katkad i bez zida; pojedine zgrade se ruše. |
| T7 | jako razorni | 84 - 95 | 300 - 342 | Velike štete na masivnim građevinama; lokomotive se prevrću; skladišta od željeznih greda djelom se urušavaju. |
| T8 | teško razorni | 96 - 107 | 343 - 385 | Posvuda urušavanje zgrada čiji dijelovi su daleko razbacani; automobili nošeni zrakom na veće udaljenosti; većina zgrada od opeke i kamena nepopravljivo uništena. |
| T9 | snažno razorni | 108 - 120 | 386 - 432 | Mnoge zgrade od armiranog betona teško oštećene; lokomotive i vlakovi podignuti u zrak i odneseni na veliku udaljenost; sva stabla i stupovi iščupani. |
| T10 | super | 121 - 134 | 433 - 482 | Čitave montažne zgrade i manje zgrade podignute u zrak i nošene na neku udaljenost. Zgrade iz armiranog betona mogu biti uništene. |
| T11 | neopisivo razorni | > 134 | > 482 | Pustošeća razaranja na velikim površinama; prevladavaju totalne štete na masivnim zgradama. |
Tropopauza
- vidi strukturu atmosfere.Troposfera
- vidi strukturu atmosfere.Turbulencija
- stanje fluida u kojem je strujanje karakterizirano nepravilnim fluktuacijama svih triju komponenti vektora brzine. Kako se komponente brzine pri turbulentnom strujanju ponašaju kao slučajne varijable (vidi sliku 1), ne možemo ih točno predvidjeti, već analiziramo njihova statistička svojstva. Pri analizi turbulencije uobičajeno je sve meteorološke varijable rastaviti na srednju vrijednost i turbulentno poremećenje. Tako npr. proizvoljnu varijablu a prikazujemo kaoa = a + a',
gdje je a prostorni ili vremenski srednjak (opisuje varijablu na promatranoj prostorno-vremenskoj skali), a a' je turbulentno poremećenje (opisuje nemjerljive utjecaje prostorno-vremenskih skala koje su manje od promatrane skale). Pojedinačna turbulentna poremećenja mogu biti velika (usporediva sa srednjakom ili čak veća od njega), a srednjak turbulentnog poremećenja je a = 0. Molekularno gibanje, na primjer, uvijek smatramo turbulentnim, budući da ne možemo mjeriti efekte pojedinačnih molekula, već samo ukupne efekte cijelog ansambla molekula. Slično, gibanja vezana uz jedan kumulus, turbulentna su sa stanovišta sinoptičke skale, pa ih u skladu s tim u jednadžbe gibanja možemo uključiti pomoću turbulentnih članova. Teorija turbulencije jedan je od najsloženijih, a istovremeno veoma važnih problema u proučavanju strujanja u fluidu.
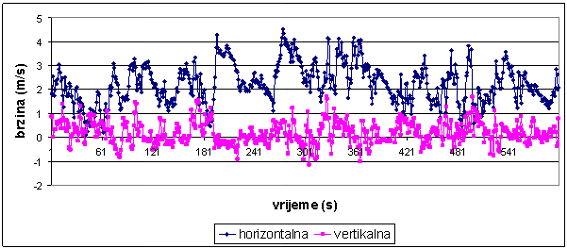
Slika 1. Desetminutni niz sekundnih vrijednosti horizontalne i vertikalne brzine vjetra izmjerene ultrasoničnim anemometrom (vidi sliku 2) u Zagrebu 12. svibnja 2004. Uočava se nepravilno, turbulentno ponašanje brzine vjetra.

Slika 2. Senzori ultrasoničnog anemometra smješteni su na terasi zgrade Geofizičkog odsjeka Prirodoslovno-matematičkog fakulteta na Horvatovcu, Zagreb.
Za turbulenciju je karakterističan širok raspon prostornih i vremenskih skala gibanja, odnosno mnoštvo turbulentnih vrtloga različitih dimenzija, koji vrlo efikasno miješaju fluid. Turbulenciju generiraju mehaničko-dinamički faktori (trenje zračne struje o prepreku i jako smicanje vjetra) te termičko-uzgonski faktor (slobodna konvekcija do koje dolazi zbog uzgona). Turbulencija je jedno od osnovnih obilježja atmosferskog graničnog sloja. U većim visinama javlja se povremeno i mjestimično, (npr. pri pojavi mlazne struje) ili u kumulonimbusu (čiji nastanak pospješuje). Za zrakoplove je naročito opasna bezoblačna turbulencija s jakim smicanjem vjetra koja se javlja na visinama od 6 do 15 km blizu jezgre mlazne struje, u blizini kumulonimbusa ili jako razvijenih kumulusa (kumulusa congestusa). Takva turbulencija nastaje zbog Kelvin-Helmholtzove nestabilnosti te sadži vrtloge raznih veličina i trajanja. Premda je kratkotrajna, uzrokuje podrhtavanje, a katkad i jako propadanje zrakoplova tijekom leta.
Vidi turbulentno strujanje, laminarno strujanje.
Više o turbulenciji možete saznati iz:
• Kundu, P. K., 1990: Fluid mechanics. Academic Press, New York, 638 str.
• Stull, R. B., 1988: An Introduction to Boundary Layer Meteorology. Kluwer Academic Publishers, Dodrecht, 666 str.
Turbulentno strujanje
- strujanje fluida koje je karakterizirano turbulencijom. Turbulentna strujanja su prostorno i vremenski jako nepravilna i isprekidana te se ponašaju poput slučajnih procesa. U turbulentnom toku dominiraju poremećenja (odstupanja od srednjeg strujanja) koja potpuno deformiraju osnovnu struju.Prijelaz iz laminarnog u turbulentno strujanje događa se kad tok postane dinamički nestabilan, odnosno kad Richardsonov broj Ri bude manji od kritične vrijednosti Ric. Najčešće se uzima Ric = 0.25, premda neka istraživanja sugeriraju i druge vrijednosti Ric u rasponu od 0.2 do 1.0.
Turbulentno strujanje prelazi u laminarno pri Ri > 1.0.
Vidi turbulencija, laminarno strujanje, Richardsonov broj.